Question
Question: Two batteries of e.m.f. \( 4V \) and \( 8V \) with internal resistance \( 1\Omega \) and \( 2\Omega ...
Two batteries of e.m.f. 4V and 8V with internal resistance 1Ω and 2Ω respectively are connected to an external resistance R=9Ω as shown in figure. The current in circuit and potential difference between P and Q respectively will be:
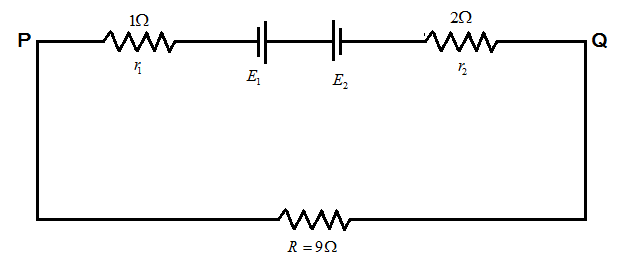
(A) 91A,9V
(B) 21A,12V
(C) 31A,3V
(D) 61A,4V
Solution
Hint : Here, the given circuit diagram has batteries connected opposite to each other. Then we have to find the net potential difference, resistance and then total current flowing in the circuit by using ohm’s law. Ohm’s law states that V=IR .
Complete Step By Step Answer:
Let us consider the figure given above such that the batteries are connected in reverse polarities or opposite to each other as shown in the figure above.
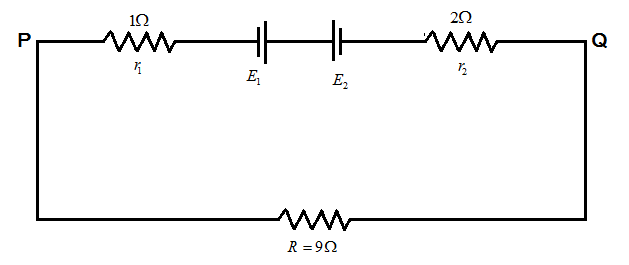
Thus, the net potential difference applied in the circuit, V′ is given by:
V′=8V−4V=4V
Now, we have to evaluate the total or net resistance applied in the circuit so that we can calculate the total current flowing through the circuit.
Net resistance is R′=R+r1+r2
⇒R′=9Ω+1Ω+2Ω
⇒R′=12Ω
Now, we can calculate the current flowing in the circuit such that we have net potential difference applied and also the net resistance in the circuit so it is possible now to calculate the net current flowing in the circuit.
It is given by the Ohm’s law:
V′=IR′
⇒I=R′V′
⇒I=12Ω4V
∴I=31A
Thus the net current flowing in the given circuit is calculated as 31A
Now, it has also asked about the potential flowing across P and Q with resistance R=9Ω .
Then,
V=IR=31A×9Ω=3V
That is potential across P and Q is 3V
The correct answer obtained is current in the circuit as 31A and the potential difference across P and Q through external resistance is 3V .
Thus the correct answer is option C.
Note :
Here, we see that the batteries are connected opposite to each other so the net potential obtained is 4V since one of the batteries is negative and the other is positively connected we can understand this concept when we see the circuit. Then we obtained the net resistance on adding all the resistances and then we calculated current by using ohm’s law. Be careful while using the signs on the batteries while adding them.
