Question

Two batteries of different $emf$ and internal resistances connected in series with each other and with an external load resistor. The current is $3A$ . When the polarity of one battery is reversed, the current becomes $1A$ . The ratio of the $emf$ of the two batteries is:
(A) $2.5:1$
(B) $2:1$
(C) $3:2$
(D) $1:1$

Answer 1

We will use Kirchhoff's rule to find a relation of the resistances and the $emf$ of the two batteries. Then, we will equate them with each other.

Step By Step Solution

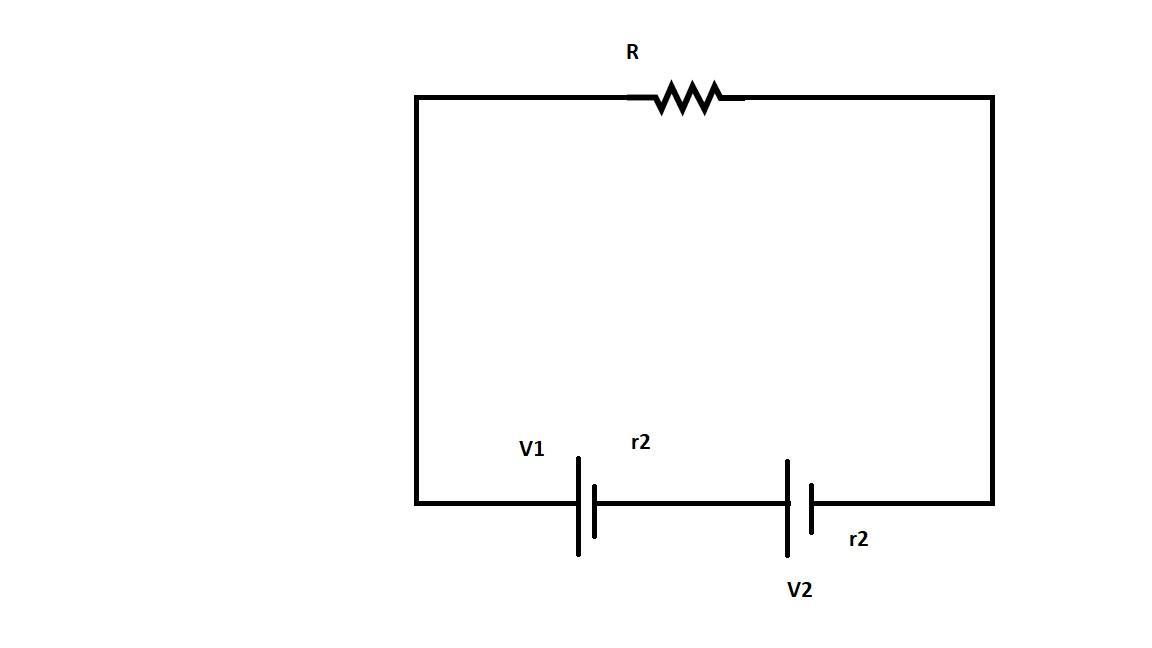
Here,
${V_1}$ is the $emf$ of the first battery and ${V_2}$ is that of the second one. ${r_1}$ is the internal resistance of the first battery and ${r_2}$ is that of the second. $R$ in the load resistance.
Now,
For the first situation when current is $3A$ .
By Kirchhoff’s Law,
$\frac{{\mathop V\nolimits_1 \mathop { + V}\nolimits_2 }}{{\mathop {R + r}\nolimits_1 \mathop { + r}\nolimits_2 }} = \mathop 3\nolimits_{}$
Thus, we can say
$\mathop {(R + r}\nolimits_1 \mathop { + r}\nolimits_2 ) = \frac{{\mathop V\nolimits_1 \mathop { + V}\nolimits_2 }}{3} \cdot \cdot \cdot \cdot (1)$
Similarly for the second case when current is $1A$ ,
$\mathop V\nolimits_1 \mathop { - V}\nolimits_2 = \mathop {R + r}\nolimits_1 \mathop { + r}\nolimits_2$
Now,
Putting in equation $(1)$, we get
$\mathop {3V}\nolimits_1 \mathop { - 3V}\nolimits_2 = \mathop V\nolimits_1 \mathop { + V}\nolimits_2$
After further evaluation, we get
$\mathop {2V}\nolimits_1 = \mathop {4V}\nolimits_2$
In the question, it is asked for $\frac{{\mathop V\nolimits_1 }}{{\mathop V\nolimits_2 }}$
Thus, we get
$\frac{{\mathop V\nolimits_1 }}{{\mathop V\nolimits_2 }} = \frac{2}{1}$

Hence, the answer is (B).

Additional Information: The Kirchhoff’s rules are handy to use in the cases for internal resistance, multiple $emf$ and in the cases indulging potentiometer. These rules are simple and very intuitive. Just that they were placed in a standardized manner by Kirchhoff.
The internal resistance we are talking about is referring to the resistance offered by the battery itself at initiation. This internal resistance value decides about the behavior of the circuit. Though minimal, but still of concern.

Note: We directly evaluated the result due to the application of the Kirchhoff’s law. One should not be confused about the direct relation. It is trivially coming from Kirchhoff's law.