Question

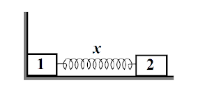
Two bars of masses ${{m}_{1}}$​ and ${{m}_{2}}$​ connected by a weightless spring of stiffness $k$ (figure shown above) rest on a smooth horizontal plane. Bar 2 is shifted a small distance$x$ to the left and then released. If the velocity of the centre of inertia of the system after bar 1 breaks off the wall is given as ${{v}_{cm}}=\dfrac{sx\sqrt{{{m}_{2}}k}}{\left( {{m}_{1}}+{{m}_{2}} \right)}$. Find $s$.

Answer 1

Motion of two blocks spring system is observed through the centre of mass frame of reference of the system. We will apply the work energy theorem on the system to determine the velocity of bar 2. For calculating the velocity of centre of mass of the system, we will use the expression relating velocity of COM to the individual velocities of the two masses.

Formula used:
Velocity of centre of mass,
${{v}_{CM}}=\dfrac{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}{{{m}_{1}}+{{m}_{2}}}$

Complete step by step answer:
We are given that two bars of masses ${{m}_{1}}$​ and ${{m}_{2}}$​ connected by a weightless spring of stiffness $k$ and bar 2 is shifted by a small distance $x$ to the left and then released.
Let x be compression in the spring when the bar ${{m}_{2}}$ is about to shift. Therefore at this moment spring force on ${{m}_{2}}$ is equal to the limiting friction between the bar ${{m}_{2}}$ and horizontal floor.
After releasing, the block ${{m}_{2}}$ acquires the velocity ${{v}_{2}}$
Applying work energy theorem for ${{m}_{2}}$
$\dfrac{1}{2}{{m}_{2}}{{\left( {{v}_{2}} \right)}^{2}}=\dfrac{1}{2}k{{x}^{2}}$
Where,
${{m}_{2}}$ is the mass of bar 2
${{v}_{2}}$ is the velocity of bar 2
$k$ is the spring constant
$x$ is the displacement of bar 2
We get,
${{\left( {{v}_{2}} \right)}^{2}}=\dfrac{k{{x}^{2}}}{{{m}_{2}}}$
Or,
${{v}_{2}}=x\sqrt{\dfrac{k}{{{m}_{2}}}}$
Velocity of centre of mass is given as,
${{v}_{CM}}=\dfrac{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
Where,
${{m}_{1}}$ is the mass of first particle
${{m}_{2}}$ is the mass of second particle
${{v}_{1}}$ is the velocity of first particle
${{v}_{2}}$ is the velocity of second particle
Putting values,

$\begin{aligned} & {{v}_{1}}=0 \\\ & {{v}_{2}}=x\sqrt{\dfrac{k}{{{m}_{2}}}} \\\ \end{aligned}$

We get,

$\begin{aligned} &{{v}_{CM}}=\dfrac{{{m}_{1}}\left(0\right)+{{m}_{2}}x\sqrt{\dfrac{k}{{{m}_{2}}}}}{{{m}_{1}}+{{m}_{2}}} \\\ & {{v}_{CM}}=\dfrac{{{m}_{2}}x\sqrt{\dfrac{k}{{{m}_{2}}}}}{{{m}_{1}}+{{m}_{2}}} \\\ \end{aligned}$

Or,
${{v}_{CM}}=\dfrac{x\sqrt{k{{m}_{2}}}}{{{m}_{1}}+{{m}_{2}}}$
Comparing above expression with given expression,
${{v}_{cm}}=\dfrac{x\sqrt{k{{m}_{2}}}}{{{m}_{1}}+{{m}_{2}}}=\dfrac{sx\sqrt{{{m}_{2}}k}}{\left( {{m}_{1}}+{{m}_{2}} \right)}$
We get,
$s=1$
The value of $s$ is 1.

Additional Information:
Block – spring system presents an approximation of SHM. It is assumed that spring force follows Hooke’s law and there are no dissipating forces like friction or air drag.
When two blocks are connected with a spring, initially the system is at rest. If one of the blocks is pulled with some force and spring elongates, it causes the other block to move as well. The displacement of two blocks can be different depending upon their respective masses. We usually observe the spring-block system through the frame of reference of the centre of mass of the system. Work energy theorem states that the work done by net forces acting on a system is equal to the change in total kinetic energy of the system.

Note:
When two blocks connected by a spring move under mutual interaction, the force interaction between the two blocks can be considered as internal forces if we take the two blocks plus spring as the system since there is no external force acting on this system.
Remember that the velocity of bar 1 is considered as zero because we have to calculate the velocity of the centre of mass of the system at the moment when the bar 1 just breaks off the wall.