Question
Question: Two balls, \(X\), and \(Y\) move along a horizontal frictionless surface, as illustrated in fig. Bal...
Two balls, X, and Y move along a horizontal frictionless surface, as illustrated in fig. Ball X has an initial velocity 3.0ms−1in a direction along line AB. Ball Yhas a mass of 2.5kgand an initial velocity 9.6m/s−1in the direction at an angle of 60∘ to line AB.
The two balls collide at the point B. The balls stick together and then travel along the horizontal surface in a direction at right-angles to the line AB, as shown in Fig. Determine the difference between the initial kinetic energy of the ball X and the initial kinetic energy of the ball Y.
The difference in kinetic energy=________________J.
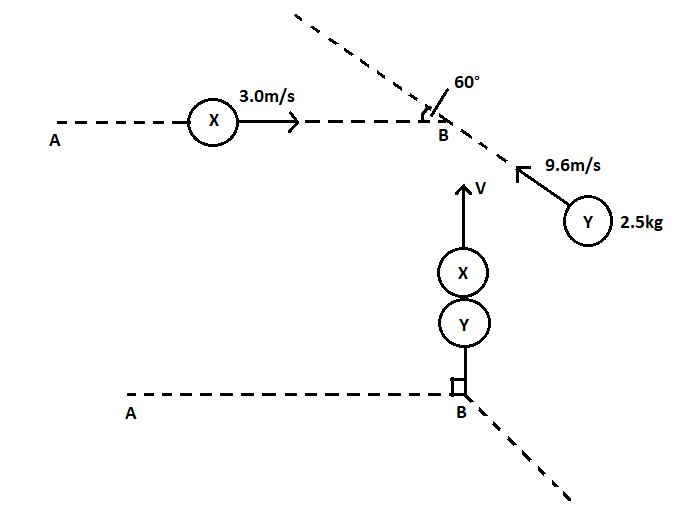
Solution
Hint We have two balls moving on a frictionless horizontal surface. The masses and velocities of the two balls are given. If the two balls collide at a given point the balls will stick together as shown in the figure and move in a direction perpendicular to the horizontal surface. We have to find the difference in kinetic energy.
Formula used
KE=21mv2
Where KE is the kinetic energy, m stands for the mass of the body, and v stands for the velocity of the body.
Complete Step by step solution
To find the difference in kinetic energy, first, we have to find the mass of the ball X
The initial velocity of X=3.0m/s
The initial velocity of Y=9.6m/s
The angle betweenAand B are given as.60∘
By applying the force on a free body diagram
After the collision, the net force will be zero
i.e. ∑F=0
This means that the change in momentum will be zero
We can write the change in momentum as,
mxvx−myvy (∵P=mv)
Where mx,myand, vx vyare the masses and velocities of the two balls Xand Yrespectively.
vycosθis the velocity component of the ball Yin the xdirection.
vx=3.0m/s
my=2.5kg
vy=9.6m/s
θ=60∘
Substituting the values in the above equation, we get mxas
(m×3.0)−(2.5×9.6×cos60∘)=0
From this,
3m=12
⇒m=312=4kg
Now that we have the masses and velocities of the two balls we can find the difference in kinetic energies.
We know that the kinetic energy of a body is,
KE=21mv2
The difference in kinetic energies can be written as,
ΔKE=21m2v22−21m1v12
Substituting the values of masses and velocities, we get
ΔKE=(21×2.5×9.62)−(21×4×3.02)
ΔKE=2230.4−236
⇒ΔKE=115.2−18=97.2
Therefore, the difference in kinetic energy =97.2J
Note
Collisions are of two types. If the total kinetic energy of the system is conserved after the collision such collisions can be called elastic collisions. If the kinetic energy of the system is not conserved after collision such collisions are called inelastic collisions. The total linear momentum of the system will be conserved in all collisions.
