Question

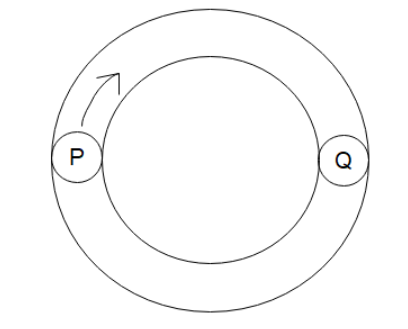
Two balls P and Q are at opposite ends of the diameter of a frictionless horizontal circular groove. P is projected along the groove and at the end of $T$second, it strikes ball Q. Let difference in their final velocities be proportional to the initial velocity of ball P and coefficient of proportionally is “e” then second strike occurs at:

A) $\dfrac{{2T}}{e}$
B) $\dfrac{e}{{2T}}$
C) $2eT$
D) $Te$

Answer 1

In this solution, we will first determine the velocity of the second ball Q when struck by the ball P. The time between the collisions can be determined by the time period of revolution of an object in a circular orbit.

Complete step by step answer:
We’ve been told that ball P is projected along the grove and at the end of “T” seconds, it collides with ball Q. Let us assume that the ball P is moving with velocity $u$. Then the velocity of the ball will be equal to the ratio of the circumference of the circle and the time it takes to cover around which will be $2T$.
$u = \dfrac{{2\pi R}}{{2T}}$
Now when the ball P collides with ball Q after $T$ seconds, it will lose some velocity, and ball Q will gain some velocity. We’ve been told that the difference of these velocities is proportional to the difference in the velocity and the coefficient of proportionality is $e$. So, assuming the new velocity of ball P as $v$ and of ball Q as $v'$, we can write
$v - v' = eu$
Now when the balls collide, ball Q will be moving with a velocity with respect to the ball P. For them to collide again, they have to cover a distance equal to the circumference of the circle (as ball Q is faster) and they will have a relative velocity of $v - v'$. Hence the time taken in this process will be
$t = \dfrac{{2\pi R}}{{v - v'}}$
Since $v - v' = eu$, we can write
$t = \dfrac{{2\pi R}}{{eu}}$ and as $u = \dfrac{{2\pi R}}{{2T}}$, we can write
$t = \dfrac{{2\pi R \times T}}{{e(2\pi R)}}$

$\Rightarrow t = \dfrac{{2T}}{e}$ which corresponds to option (A).

Note: While calculating the time taken by the second collision, we must realize that the ball Q will move faster than ball P. To further simplify the problem, we should treat them as one relative object that has to cover a distance equal to the circumference of the circle while travelling with a relative velocity that is equal to the difference of their velocities.