Question

Two balls of equal masses are thrown upwards along the same vertical direction at an interval of $2s$, with the same initial velocity of $39.2m{s^{ - 1}}$. The two balls will collide at a height of
A). $39.2m$
B). $73.5m$
C). $78.4m$
D). $117.6$

Answer 1

Hint – Start by drawing a well-labelled diagram that clearly describes the situation. Then use equations of motion to obtain the exact time taken by the two balls and then use given velocity and time to calculate the height of the point of collusion.

Complete step-by-step solution -
The diagram of the situation below

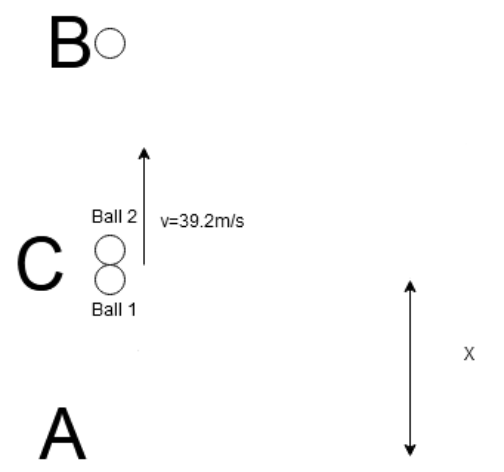
In this diagram $A$is the starting point of both the balls. $B$ is the highest point that the first ball would reach, $C$ is the point of collision.
Given in the problem,
$u = 39.2m{s^{ - 1}}$,
Time till the 1st ball collides with the 2nd ball $({t_1}) = t\sec$
Time till the 2nd ball collides with the 1st ball $({t_2}) = ({t_1} - 2)\sec$
Let’s assume that the two balls collide t sec later, and the height of the point of collusion (point) from the ground is x.
Applying the second equation of motion to the first ball, we get
$\Rightarrow s = ut + \dfrac{{a{t}^2}}{2}$
$\Rightarrow x = 39.2 \times {t_1} + \dfrac{1}{2}gt_1^2$ (Here gravity is acting as the sole source of external force on the ball)
$\Rightarrow x = 39.2{t_{ 1}} + \dfrac{{gt_1^2}}{2}$ (Equation 1)
Applying the second equation of motion to the second ball, we get
$S = ut - \dfrac{1}{2}a{t^2}$
$\Rightarrow x = 39.2 \times {t_2} - \dfrac{1}{2}gt_2^2$
$\Rightarrow x = 39.2{t_2} - \dfrac{1}{2}gt_2^2$
$\Rightarrow x = 39.2({t_1} - 2) - \dfrac{1}{2}g{({t_1} - 2)^2}$ $(\because {t_2} = {t_1} - 2)$ (Equation 2)
Substituting the value of x from equation 1 in equation 2, we get
$39.2{t_1} - \dfrac{1}{2}gt_1^2 = 39.2({t_1} - 2) - \dfrac{1}{2}g{({t_1} - 2)^2}$
$\Rightarrow 39.2{t_1} - \dfrac{1}{2}gt_1^2 = 39.2{t_1} - 78.4 - \dfrac{1}{2}gt_1^2 - 2g + 2g{t_1}$
$\Rightarrow 2g({t_1} - 1) = 78.4$
$\Rightarrow 2 \times 9.8({t_1} - 1) = 78.4$
$\Rightarrow {t_1} - 1 = 4$
$\Rightarrow {t_1} = 5\sec$
Now, for calculating the distance of the point of collision from the ground $(x)$, we simply use the equation of speed for the second ball, i.e.
Speed=$\dfrac{x}{{{t_2}}}$
$\Rightarrow v = \dfrac{x}{{{t_1} - 2}}$
$\Rightarrow 39.2 = \dfrac{x}{3}$
$\Rightarrow x = 117.6m$
Hence, option D is the correct option.

Note – In this type of problems, we usually ignore possible interfering factors such as air resistance, and gravitational pull of other celestial objects, unless stated otherwise. In practical, the balls would face these ignored factors and this will if not greatly, to some extent cause a variability in the results obtained.