Question

Two balls of different masses $m_1$ and $m_2$ are dropped from different heights $h_1$ and $h_2$ respectively. The ratio of the time taken by the two balls to fall through this distance is ____.

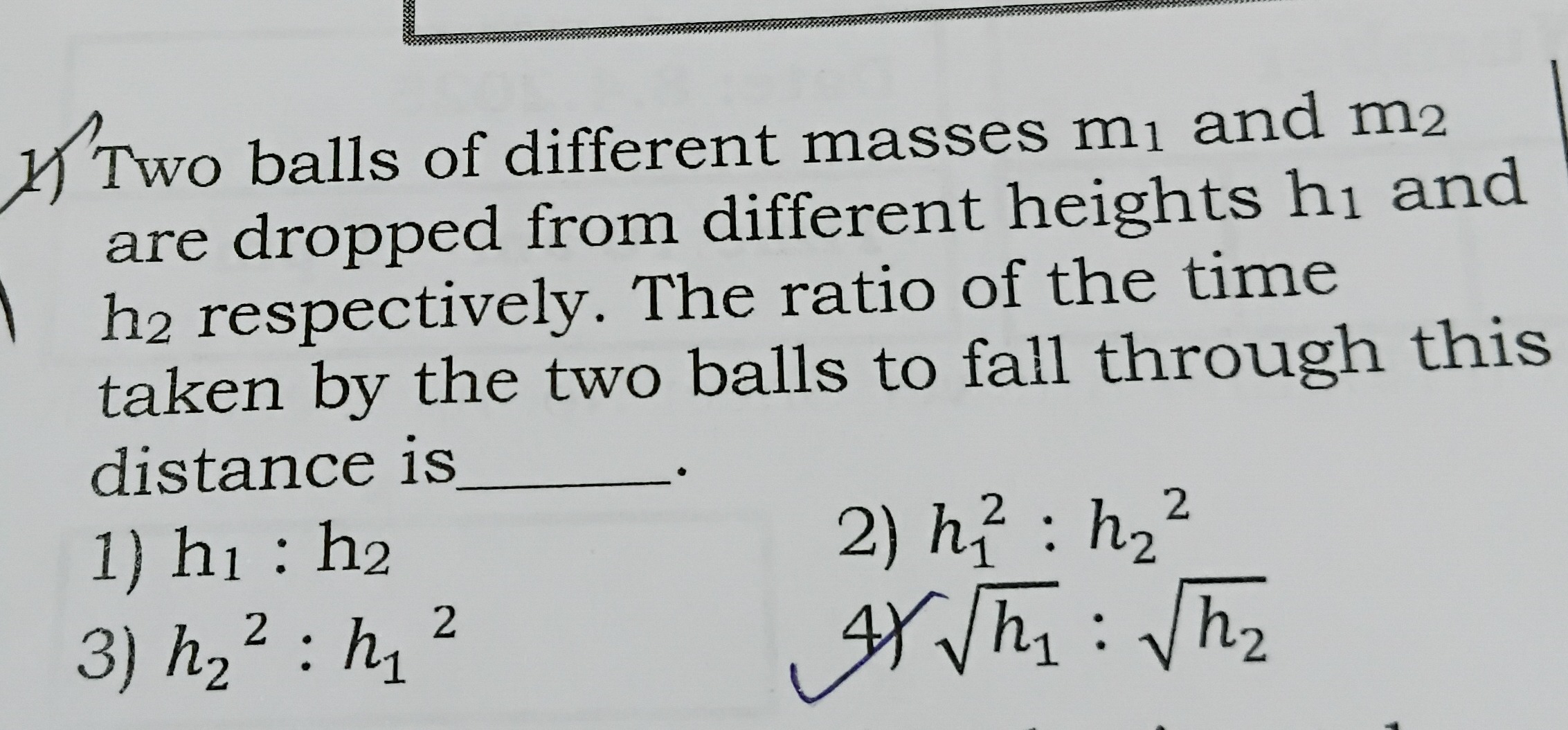
• A. $h_1 : h_2$
• B. $h_1^2 : h_2^2$
• C. $h_2^2 : h_1^2$
• D. $\sqrt{h_1} : \sqrt{h_2}$

Answer 1

Answer: (D)

$\sqrt{h_1} : \sqrt{h_2}$

Answer 2

For an object in free fall from rest,

$h = \frac{1}{2} g t^2 \quad \Rightarrow \quad t = \sqrt{\frac{2h}{g}}$.

Thus, the time taken by the two balls are:

$t_1 = \sqrt{\frac{2h_1}{g}} \quad \text{and} \quad t_2 = \sqrt{\frac{2h_2}{g}}$.

The ratio of the times is:

$\frac{t_1}{t_2} = \frac{\sqrt{\frac{2h_1}{g}}}{\sqrt{\frac{2h_2}{g}}} = \sqrt{\frac{h_1}{h_2}} = \sqrt{h_1} : \sqrt{h_2}$.