Question

Two balls having same mass and charge and located on same vertical at height ${{h}_{1}}$ and ${{h}_{2}}$ are thrown in the same direction along the horizontal at the same velocity v. The first ball touches the ground at a distance $l$ from the initial vertical. At what height ${{H}_{2}}$ will the second ball be at this instant? The air drag and the effect of the charges induced on the ground should be neglected.

Answer 1

In this question, we have been told to neglect the air drag and the effect of the charges induced on the ground. So, here the only force that will be acting on the system will be gravitational force. This question can be solved by finding out the centre of mass of the system combining the two balls of equal mass. Also, the key point to remember is that the Centre of mass will follow a certain trajectory which will not be changed, hence allowing us to find the position of the second ball with the help of the given position of the first ball.

Complete step by step answer:

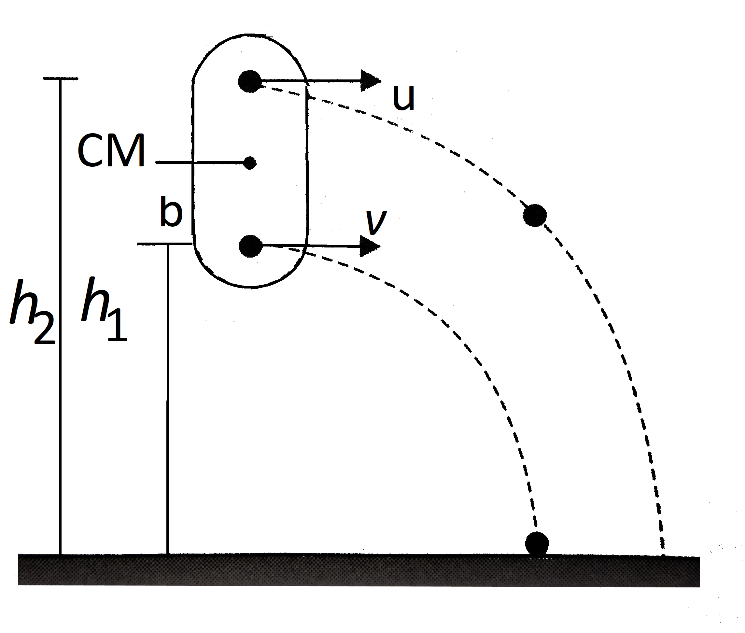
Both balls are used in our system. The free Coulomb between the two balls is an intrinsic mechanism for the mechanism. The acceleration of the centre of mass is not affected by internal forces. Only under the control of gravity does the rotation of the centre of mass take place. In a parabolic trajectory, the centre of mass moves. Since the initial velocity of the two balls is horizontal, x / v is the time taken to travel distance x and the vertical height decreases in this time by the centre of mass
$\Rightarrow y=\dfrac{1}{2}g{{(\dfrac{x}{v})}^{2}}$
Now,
Let us assume a single mechanical scheme to be the two charged balls. The contact between the balls is intrinsic to the Coulomb, and therefore it does not influence the motion of the mass core. The force of gravity is the only external force acting on the device. It is only this force that can decide the rotation of the system's centre of mass. The original position of the centre of mass is at a height $\dfrac{\left( h_1\text{ }+\text{ }h_2 \right)}{2}$, and its original velocity v is horizontal, since the masses of the balls are equal. So a parabola characterised by the following equation will travel around the centre of mass:
$\Rightarrow h=\dfrac{{{h}_{1}}+{{h}_{2}}}{2}-\dfrac{1}{2}g{{\left( \dfrac{x}{v} \right)}^{2}}$
When the first ball touches the ground at a distance x=R, the height of the centre of mass from the ground is
$h=\dfrac{{{h}_{1}}+{{h}_{2}}}{2}-\dfrac{1}{2}g{{(\dfrac{R}{v})}^{2}}$
As the masses of the balls are equal, at this moment the second ball will be ${{H}_{2}}=2h$ in height. Accordingly,
$\therefore {{H}_{2}}=({{h}_{1}}+{{h}_{2}})-g{{(\dfrac{R}{v})}^{2}}$

Note:
This same theory works in the case of fireworks. After the explosion of the fireball, the remains will move in a way such that their COM will keep following the same trajectory that it was following before the blast.