Question

Two balls each of mass undergo head on collision while each was moving with speed $6\,m{s^{ - 1}}$. If the coefficient of restitution is $\dfrac{1}{3}$, the speed of each ball after impact will be
A. $18\,m{s^{ - 1}}$
B. $2\,m{s^{ - 1}}$
C. $6\,m{s^{ - 1}}$
D. $4\,m{s^{ - 1}}$

Answer 1

First we will draw a rough diagram representing all the required parameters. We need to draw two different diagrams, first the position of balls before collision and second the position of balls after collision. Then using the condition of head on collision we can find the speed of each ball after impact. The speed of each ball will be the same as both the balls are identical and the speed before impact of two balls are the same.

Complete step by step answer:
As per the problem we have two balls each of mass undergo head on collision while each was moving with speed $6\,m{s^{ - 1}}$.If the coefficient of restitution is $\dfrac{1}{3}$.Now we need to calculate the speed of each ball after impact.

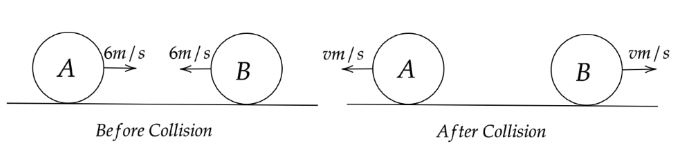
We know that,
Coefficient of restitution, $e = \dfrac{1}{3}$
Initial speed of both the balls are same, ${u_1} = {u_2} = u = 6\,m{s^{ - 1}}$
Final speed of both the ball will be same, ${v_1} = {v_2} = v\,m{s^{ - 1}}$
Now using head on collision condition we can write,
$e = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$
Now putting the given values we will get,
$\dfrac{1}{3} = \dfrac{{v - \left( { - v} \right)}}{{6 - \left( { - 6} \right)}}$
On further solving we will get,
$\dfrac{1}{3} = \dfrac{{v + v}}{{6 + 6}} = \dfrac{v}{6}$
Cancelling the common terms and rearranging we will get,
$\therefore v = 2\,m{s^{ - 1}}$

Therefore the correct option is B.

Note: Keep in mind that before solving we should know that the speed of both the balls before impact is same and at the same time speed of both the balls after impact is the same but they are in opposite directions. That's why in the above equation we take the speed of one ball to be positive and the other to be negative. If we take both in the same direction then the speed will cancel out and we will get a not definite value.