Question

Two balls A and B of same mass and a third ball C of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball $A$ moves with a velocity $v$ towards balls B and C. All collisions are assumed to be elastic. If M < m, the number of collisions between the balls will be

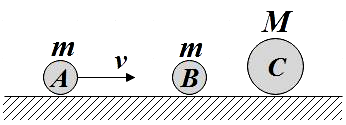
A. 1
B. 2
C. 3
D. 4

Answer 1

When ball A collides with B, the whole momentum of ball A is transferred to ball B and thus we can find their velocities after collision. The next collision happens for B and C which have unequal masses. Now we could find their respective velocities after collision and thereby find the chances of further collisions and hence the answer to the question.

Formula used:
Expressions for velocities of 2 bodies of unequal masses after collision,
${{v}_{1}}'=\dfrac{\left( {{m}_{1}}-{{m}_{2}} \right)}{\left( {{m}_{2}}+{{m}_{1}} \right)}{{v}_{1}}+\dfrac{2{{m}_{2}}}{{{m}_{2}}+{{m}_{1}}}{{v}_{2}}$
${{v}_{2}}'=\dfrac{2{{m}_{1}}}{{{m}_{2}}+{{m}_{1}}}{{v}_{1}}+\dfrac{{{m}_{2}}-{{m}_{1}}}{{{m}_{2}}+{{m}_{1}}}{{v}_{2}}$

Complete step-by-step answer:
We are given 3 balls A, B and C of masses m, m and M respectively. Ball A is moving with velocity and is colliding with ball B. Now by momentum conservation, we know that, sum of the momentums of both bodies should be constant before and after collision. Before collision, ball B has zero momentum, as both balls have the same mass ‘m’, in order for momentum to be conserved the momentum possessed by ball A should be completely transferred to ball B after collision. In other words, after collision ball A goes to rest and ball B moves with velocity v in the same direction.
Now ball B is moving with velocity v towards ball C at rest.
For 2 unequal masses ${{m}_{1}}$ and ${{m}_{2}}$ moving with velocities ${{v}_{1}}$ and ${{v}_{2}}$, the velocity of these masses after collision is respectively given by,
${{v}_{1}}'=\dfrac{\left( {{m}_{1}}-{{m}_{2}} \right)}{\left( {{m}_{2}}+{{m}_{1}} \right)}{{v}_{1}}+\dfrac{2{{m}_{2}}}{{{m}_{2}}+{{m}_{1}}}{{v}_{2}}$ …………………………………. (1)
${{v}_{2}}'=\dfrac{2{{m}_{1}}}{{{m}_{2}}+{{m}_{1}}}{{v}_{1}}+\dfrac{{{m}_{2}}-{{m}_{1}}}{{{m}_{2}}+{{m}_{1}}}{{v}_{2}}$ …………………………………… (2)
From (1), velocity of ball B after collision will be,
${{v}_{B}}'=\dfrac{m-M}{m+M}v+\dfrac{2M}{M+m}\left( 0 \right)$
For m ≪ M, ${{v}_{B}}'\approx v$
From (2), velocity of C after collision is,
${{v}_{C}}'=\dfrac{2m}{M+m}v+\dfrac{M-m}{M+m}\left( 0 \right)$
For m ≪ M, ${{v}_{C}}'\approx 2v$
So we find that ball B moves with velocity v towards right and ball C moves with velocity 2v to right. Therefore, we see that only 2 collisions take place for the system, A with B and then B with C. Hence, option B is the correct answer.

So, the correct answer is “Option B”.

Note: A collision is said to be elastic when total kinetic energies of the two bodies after collision is equal to the total kinetic energy before collision. That is, there is no net conversion of kinetic energy into other forms. In the question above if the direction of either ball B or C has been negative there exist chances for another collision with ball A which is at rest. So direction is important.