Question

Two automobiles start from point A at the same time. One travels toward the west at the speed of $60$ miles per hour while the other travels towards the North at $35mph$ . Their distance apart after $3$ hours later is increasing at the rate (in mph)
$\left( A \right)5\sqrt {193}$
$\left( B \right)\sqrt {193}$
$\left( C \right)\dfrac{5}{{\sqrt {193} }}$
$\left( D \right)\,{\text{None}}\,\,{\text{of}}\,\,{\text{these}}$

Answer 1

First as per the problem statement we need to draw a rough diagram so as to write the equation of the total distance travelled. Then on differentiating the total distance we can find the rate of increase in speed after $3$ hours.

Complete answer:
As per the given problem we know that there are two automobiles starting from point A at the same time. One travels toward the west at the speed of $60$ miles per hour while the other travels towards the North at $35mph$ .
We need to find the distance apart after $3$ hours later is increasing at the rate (in mph).

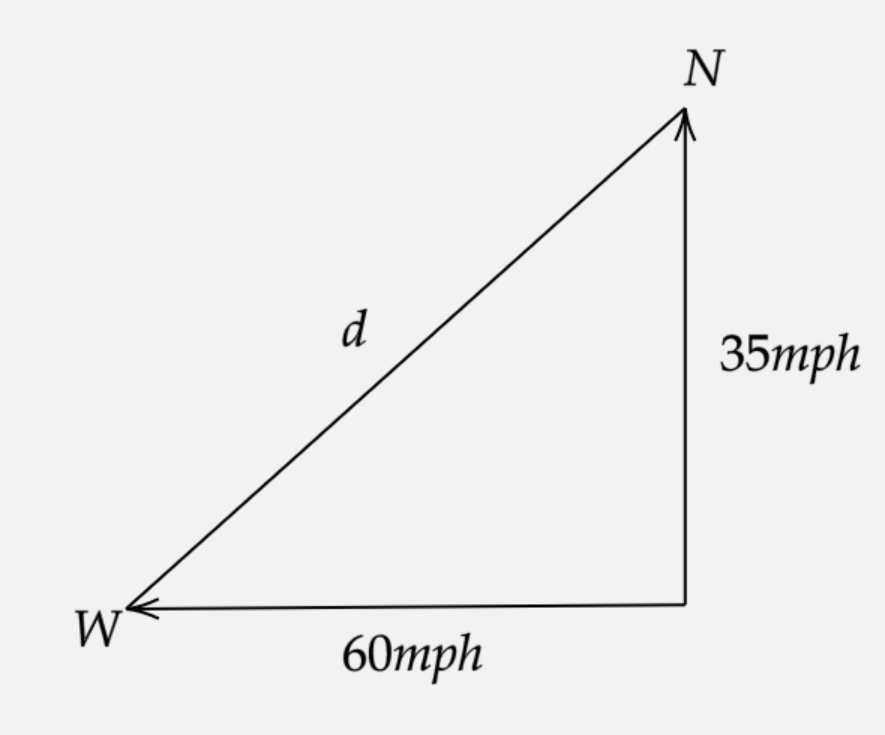
We know the speed of the two automobiles,
Distance is equal to speed multiplied with time.
Hence from the figure we can write,
${d^2} = {\left( {35t} \right)^2} + {\left( {60t} \right)^2} \ldots \ldots \left( 1 \right)$
At $t = 3hour$ we will get,
${d^2} = {\left( {35 \times 3} \right)^2} + {\left( {60 \times 3} \right)^2}$
On further solving we will get,
${d^2} = {\left( {105} \right)^2} + {\left( {180} \right)^2}$
$\Rightarrow {d^2} = 43425$
Hence the distance will be,
$d = 15\sqrt {193}$
Now on differentiating the equation $\left( 1 \right)$ wrt t we will get,
$\dfrac{{d{d^2}}}{{dt}} = \dfrac{{d{{\left( {35t} \right)}^2}}}{{dt}} + \dfrac{{d{{\left( {60t} \right)}^2}}}{{dt}}$
On further solving we will get,
$\dfrac{{d{d^2}}}{{dt}} = 1225 \times \dfrac{{d{t^2}}}{{dt}} + 3600 \times \dfrac{{d{t^2}}}{{dt}}$
$\Rightarrow 2d \times \dfrac{{dd}}{{dt}} = 1225 \times 2t + 3600 \times 2t$
Now cancelling the common terms we will get,
$d \times \dfrac{{dd}}{{dt}} = 1225 \times t + 3600 \times t$
At $t = 3$ we will get,
$d\dfrac{{dd}}{{dt}} = 1225 \times 3 + 3600 \times 3$
Taking d to other side we will get,
$\dfrac{{dd}}{{dt}} = \dfrac{{14475}}{d}$
Putting the value of $d = 15\sqrt {193}$ we will get,
$\dfrac{{dd}}{{dt}} = \dfrac{{14475}}{{15\sqrt {193} }}$
$\Rightarrow \dfrac{{dd}}{{dt}} = \dfrac{{965}}{{\sqrt {193} }}$
Multiplying and dividing $\sqrt {193}$ in RHS we will get,
$\dfrac{{dd}}{{dt}} = \dfrac{{965}}{{\sqrt {193} }} \times \dfrac{{\sqrt {193} }}{{\sqrt {193} }} = \dfrac{{965\sqrt {193} }}{{193}}$
On cancelling further we will get,
$\dfrac{{dd}}{{dt}} = 5\sqrt {193} mph$
Therefore the correct option is $\left( A \right)$ .

Note:
Remember that the rate of change of one quantity withbretapet to time can be calculated by differentiating the given function with respect to time. And we can see the rate of change is infinitesimal changes in the given quantity when there is an infinitesimal change in time. And here in this problem the distance depends on the time.