Question

Truth table for the given circuit will be

A)

x	y	Z
$0$	$0$	$1$
$0$	$1$	$1$
$1$	$0$	$1$
$1$	$1$	$0$

B)

x	y	Z
$0$	$0$	$0$
$0$	$1$	$0$
$1$	$0$	$0$
$1$	$1$	$1$

C)

X	y	Z
$0$	$0$	$1$
$0$	$1$	$1$
$1$	$0$	$1$
$1$	$1$	$1$

D)

X	Y	Z
$0$	$0$	$0$
$0$	$1$	$1$
$1$	$0$	$1$
$1$	$1$	$1$

Answer 1

In the given circuit, we have AND gates, NOT gate and NAND gate. The output for NAND gate is $0$ only when both the inputs are $1$ otherwise the output is $1$. For output for NOT is the reverse of the input. For AND gate, the output is $1$ only when both the input is $1$. Using this check the output at different points for different input and thus check the final output.

Complete step by step answer:
We are given with two AND gates, one NOT gate and the final output is given by a NAND gate. When there are $2$ inputs the total combination of input becomes ${2^2} = 4$. Let us check the output for each set of input.
The input set is: $(0,0)$, $(0,1)$, $(1,0)$, $(1,1)$.
Let us consider the output for each set:

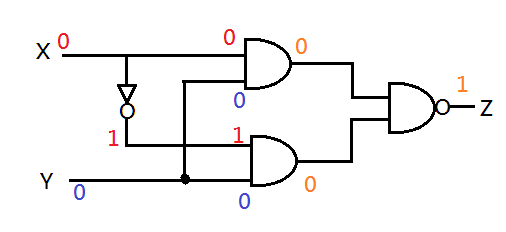
Clearly, we can see that for input set $(0,0)$ the output is $1$
For input set $(0,1)$ the output will be:

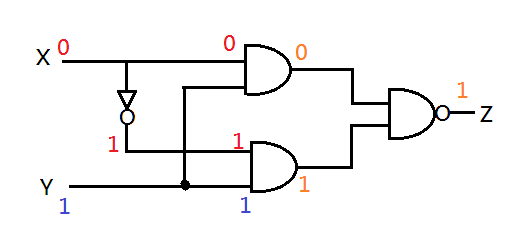
We can see that for input set $(0,1)$ the output is $1$
For input set $(1,0)$ the output will be:

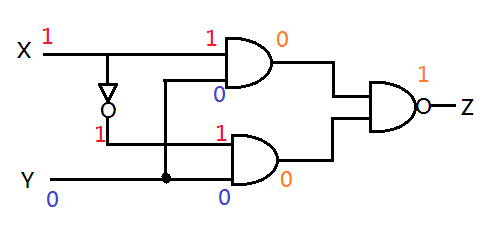
The output for $(1,0)$ is $1$.
Now, let's find the output for $(1,1)$ :

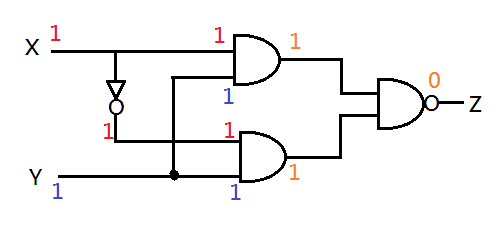
The output for $(1,1)$ is $0$.
The output set is $(1,1,1,0)$ which is in option A.

So, the correct answer is “Option A”.

Note:
In order to solve such compound logic gates problems, it is better if the output for each set is calculated individually. The output for AND gate is $1$ only if both the input is $1$. The output for NOT gate is reverse of the input. It becomes difficult to solve this problem using a truth table instead the given approach can be followed.