Question
Question: Truth table for a system of four NAND gates as shown in figure is: 
A.
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
B.
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
C.
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
D.
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Solution
Any complicated circuit should first be solved by solving it algebraically with the help of the laws given in Boolean algebra. If A and B are two inputs of a NAND gate, then its output is given by Y= (A.B)’.
Formula used: De Morgan’s law: Complement of sum is product of complement and vice versa. The expressions are:
(A+B)’=A'.B'
(A.B)’=A'+B'
Distributive law:
A+B.C= (A+B)(A+C)
These laws are specifically for Boolean algebra.
Complete step by step answer:
A NAND gate is a logic gate that has a logic circuit which produces the output as a complement of products of two or more inputs. The truth table for a two input NAND gate is given as:
| A | B | Y =(A.B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
It can be seen from the truth table that the NAND gate produces a low output only when both inputs are high. The truth table is just the complement of the AND gate truth table.
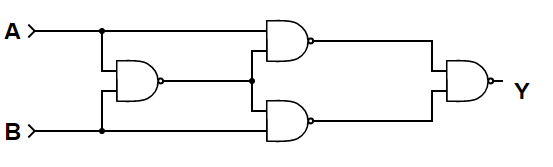
The given circuit has 4 NAND gates. The simplification can be done as:
1. From the first NAND gate on the left, we get its output as:
(A.B)’
as the inputs to the gate were A and B.
2. This output is connected as an input in the next stage. The upper NAND gate gives:
((A.B)’.A)’
which is simplified as
((A.B)’.A)’=( (A.B)’)’+A'= AB+A'.
Using distributive law, we get:
AB+A'= (A+A')(B+A')=B+A'
Similarly, the lower NAND gate produces:
Output: B'+A
The last stage of the NAND gate produces the output:
((B+A')( B'+A))’= (B+A')’+(B'+A)’=A.B'+B.A'
This can be recognized as the expression for exclusive OR gate.
The truth table for an exclusive OR gate is given as:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
So, the correct answer is “Option A”.
Note: The input connections should be noted down carefully. It might change the result entirely even if the primed part is missing. The truth table for NAND gate can be remembered as the complement of AND gate truth table.
