Solveeit Logo
Login

Question

Question: The value of the expression $2sec^{-1}2 + sin^{-1}(\frac{1}{2})$ is...

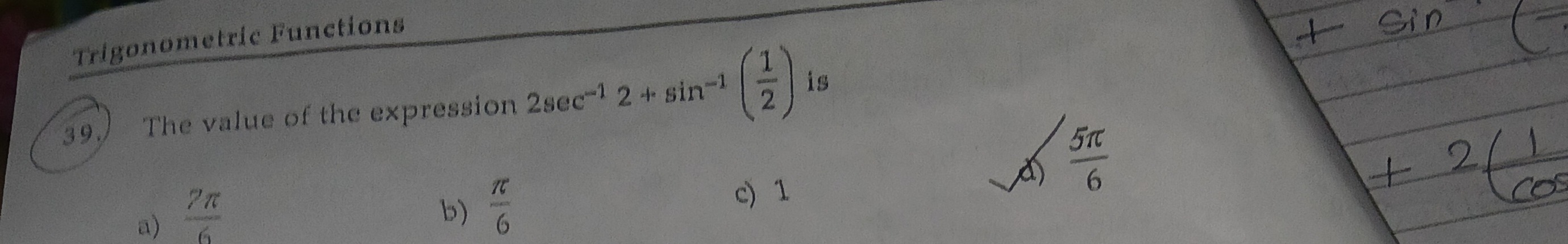
The value of the expression 2sec−12+sin−1(12)2sec^{-1}2 + sin^{-1}(\frac{1}{2}) is

A

7π6\frac{7\pi}{6}

B

π6\frac{\pi}{6}

C

1

D

5π6\frac{5\pi}{6}

Answer

5π6\frac{5\pi}{6}

Explanation

Solution

Let

θ=sec⁡−1(2). Then sec⁡θ=2  ⟹  cos⁡θ=12,0≤θ≤π (θ≠π2).\theta = \sec^{-1}(2). \text{ Then } \sec\theta = 2 \implies \cos\theta = \frac{1}{2},\quad 0 \le \theta \le \pi \, (\theta \neq \frac{\pi}{2}).

Thus, θ=π3\theta = \frac{\pi}{3}.

So,

2sec⁡−1(2)=2(π3)=2π3.2\sec^{-1}(2) = 2\left(\frac{\pi}{3}\right) = \frac{2\pi}{3}.

Also,

sin⁡−1(12)=π6.\sin^{-1}\left(\frac{1}{2}\right) = \frac{\pi}{6}.

Adding these, we get:

2sec⁡−1(2)+sin⁡−1(12)=2π3+π6=4π6+π6=5π6.2\sec^{-1}(2) + \sin^{-1}\left(\frac{1}{2}\right) = \frac{2\pi}{3} + \frac{\pi}{6} = \frac{4\pi}{6} + \frac{\pi}{6} = \frac{5\pi}{6}.