Question

Triangle ABC is drawn in the Cartesian plane. The coordinates of A is (3,-5), the coordinates of B is (-7,4) and the coordinates of its centroid is (2,-1). Find the coordinate of vertex C.

Answer 1

Hint: Use the theorem of geometry that centroid divides all the medians in the ratio of 2 : 1. Median is the line segment through the vertex and midpoint of the opposite side.
Use section formula of line segment,

If a line AB has coordinate of A = (a,b) and B = (c,d), then the coordinate of point P which divide the line segment AB in the ratio m : n is

$\begin{aligned} & x\,\text{coordinate of P = }\dfrac{an+cm}{m+n} \\\ & y\,\text{coordinate of P = }\dfrac{bn+dm}{m+n} \\\ \end{aligned}$

Complete step-by-step answer:

First let us draw the figure on the basis of information given in the question.

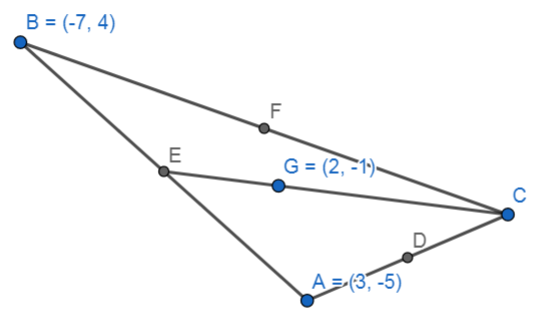
We are given that the coordinate of A is (3, -5) and the coordinate of B is (-7,4).
CE is the median and G is the centroid of triangle ABC with the coordinate (2,-1).
We know that centroid is the intersection of all the three medians therefore it lies on the median CE.
We also know that the centroid divides the median in the ratio 2 : 1.
So, centroid G divides CE in the ratio 2 : 1.
Now since CE is a median it implies that E is the midpoint. That means E divides the line AB in the ratio 1 :1. So calculating the coordinates of E using section formula which says that
If a line AB has coordinate of A = (a,b) and B = (c,d), then the coordinate of point P lying between AB which divide the line segment AB in the ratio m : n is
$\begin{aligned} & x\,\text{coordinate of P = }\dfrac{an+cm}{m+n} \\\ & y\,\text{coordinate of P = }\dfrac{bn+dm}{m+n} \\\ \end{aligned}$
Coordinate of point E is
$\begin{aligned} & x\,\text{coordinate of E = }\dfrac{3(1)+(-7)(1)}{2}=-2 \\\ & y\,\text{coordinate of E = }\dfrac{(-5)(1)+(4)(1)}{2}=\dfrac{-1}{2} \\\ \end{aligned}$
So, $E=\left( -2,\dfrac{-1}{2} \right)$
Let the coordinate of C be (i,j). Then we apply the section formula on the line segment CE with point G dividing CE in the ratio 2 : 1.
$\begin{aligned} & x\,\text{coordinate of G = }\dfrac{2(-2)+1(i)}{3}=\dfrac{-4+i}{3} \\\ & y\,\text{coordinate of G = }\dfrac{2\left( \dfrac{-1}{2} \right)+1(j)}{3}=\dfrac{-1+j}{3} \\\ \end{aligned}$
The coordinate of G is given as (2,-1).
So we get,
$\begin{aligned} & 2=\dfrac{-4+i}{3} \\\ & \Rightarrow -4+i=6 \\\ & \Rightarrow i=10 \\\ \end{aligned}$
and
$\begin{aligned} & -1=\dfrac{-1+j}{3} \\\ & \Rightarrow -1+j=-3 \\\ & \Rightarrow j=-2 \\\ \end{aligned}$
So the coordinate of C is $(10,-2)$.

Note: You can also use the formula used for calculating the coordinates of centroid when the coordinate of all the vertices of the triangle is given.
If triangle ABC has a coordinates $A=({{x}_{1}},{{y}_{1}})\,,\,B=({{x}_{2}},{{y}_{2}})\,,\,C=({{x}_{3}},{{y}_{3}})$ then the coordinates of its centroid G can be calculated by
$\begin{aligned} & x\,\text{coordinate of G = }\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \\\ & y\,\text{coordinate of G = }\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \\\ \end{aligned}$
In the question coordinates of centroid and two vertices are given. So putting those values in the above equations we can solve for coordinates of vertex C.
$\begin{aligned} & 2=\dfrac{3-7+{{x}_{3}}}{3} \\\ & \Rightarrow {{x}_{3}}-4=6 \\\ & \Rightarrow {{x}_{3}}=10 \\\ & \text{and} \\\ & -1=\dfrac{-5+4+{{y}_{3}}}{3} \\\ & \Rightarrow {{y}_{3}}-1=-3 \\\ & \Rightarrow {{y}_{3}}=-2 \\\ \end{aligned}$
So coordinates of C is (10,-2).