Question

Triangle ABC is a right triangle such that $AB=AC$ and bisector of angle $C$ intersects the sides $AB$ at $D$. Prove that $AC+AD=BC$.

Answer 1

In this question we have been given with a right triangle $\Delta ABC$, for which the length of $AB=AC$ and the triangle is right-angled at $\angle A$. We will solve this question by using the Pythagoras theorem to get the value of the hypotenuse and then use the property of angle bisector theorem to get the ratio of sides. We will then simplify the expression and get the required solution.

Complete step by step answer:
We know that $\Delta ABC$ is a right triangle such that $AB=AC$ and there is an angle bisector present at angle $C$ which intersects at the side $AB$ at a point $D$.
We can draw the diagram as:

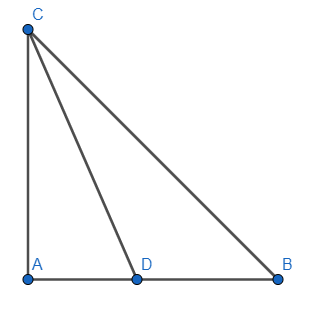
Now in $\Delta ABC$, using Pythagoras theorem, we get:
$\Rightarrow A{{B}^{2}}+A{{C}^{2}}=C{{B}^{2}}$
Now we know that $AB=AC$, consider the length be $x$, on substituting, we get:
$\Rightarrow {{x}^{2}}+{{x}^{2}}=C{{B}^{2}}$
On adding the terms on the left-hand side, we get:
$\Rightarrow 2{{x}^{2}}=C{{B}^{2}}$
On taking the square root on both the sides, we get:
$\Rightarrow \sqrt{2}x=CB$
Now we know the length of $BD$ as:
$\Rightarrow BD=AB-AD$
Let the value of $AD=b$ therefore, we get:
$\Rightarrow BD=a-b$.
Now in the given triangle, by angle bisector theorem, we know that the ratio of the adjacent sides of the bisected angle and the ratio of the line segments formed at the point where the bisector intersects is equal, we can write:
$\Rightarrow \dfrac{AD}{BD}=\dfrac{AC}{BC}$
On substituting the values, we get:
$\Rightarrow \dfrac{b}{a-b}=\dfrac{a}{a\sqrt{2}}$
On simplifying, we get:
$\Rightarrow \dfrac{b}{a-b}=\dfrac{1}{\sqrt{2}}$
On rearranging the terms, we get:
$\Rightarrow b=\dfrac{a}{1+\sqrt{2}}$
On rationalizing the denominator, we get:
$\Rightarrow b=\dfrac{a}{1+\sqrt{2}}\times \dfrac{1-\sqrt{2}}{1-\sqrt{2}}$
On simplifying, we get:
$\Rightarrow b=\dfrac{a\left( 1-\sqrt{2} \right)}{1-2}$
On simplifying, we get:
$\Rightarrow b=\dfrac{a\left( 1-\sqrt{2} \right)}{-1}$
On taking the negative sign in the numerator, we get:
$\Rightarrow b=a\left( \sqrt{2}-1 \right)$
On simplifying, we get:
$\Rightarrow b=a\sqrt{2}-a$
On rearranging, we get:
$\Rightarrow a+b=a\sqrt{2}$
Now we know that $AC=a$, $AD=b$ and $BC=a\sqrt{2}$ therefore, we get:
$\Rightarrow AC+AD=BC$, hence proved.

Note: In this question we have used the Pythagoras theorem followed by the angle bisector theorem to get the required solution. It is to be remembered that when taking the square root on both sides, only the positive root is considered since length cannot be negative. To solve these types of questions, diagrams should be made for simplification.