Solveeit Logo
Login

Question

Question: Triangle ABC has \[AC = 8x - 3,{\text{ }}BC = 4x - 1,\] angle \[ABC = 120\] and angle \[ACB = 15.\] ...

Triangle ABC has AC=8x−3, BC=4x−1,AC = 8x - 3,{\text{ }}BC = 4x - 1, angle ABC=120ABC = 120 and angle ACB=15.ACB = 15. Show that the exact value of x  is  (9+sqrt6)x\;{\text{is}}\;\left( {9 + sqrt6} \right) divided by 20.

Explanation

Solution

First either find the equation of the third side AC, or the angle BAC, and then use sine rule for triangles that can be understood as the ratio of length of side to sine of its opposite angle is equal to the ratio of length of other sides to their respective sine of opposite angles.

Complete step by step solution:
We can prove the given question with the help of sine rule for triangles.
Let us understand what sine rule for triangle says,
In a ΔABC,\Delta ABC,

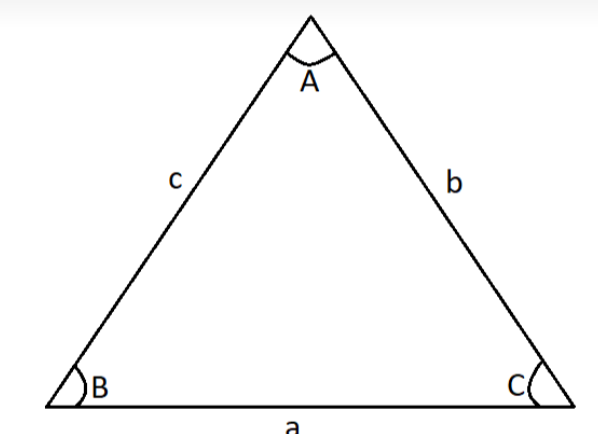
Where a,  b  and  c{\text{a,}}\;{\text{b}}\;{\text{and}}\;{\text{c}} are its sides and
A, B  and  C{\text{A,}}\,{\text{B}}\;{\text{and}}\;{\text{C}} are its angles, sine rule is given as
asinA=bsinB=csinC\dfrac{{\text{a}}}{{{\text{sinA}}}} = \dfrac{{\text{b}}}{{{\text{sinB}}}} = \dfrac{{\text{c}}}{{{\text{sinC}}}}
In order to apply this rule we should have at least two pairs of angles and their respective sides, but here in the question we have one pair only, that is AC=8x−3  and  ∠ABC=1200AC = 8x - 3\;and\;\angle ABC = {120^0}
We have to find angle BAC, in order to have the another pair
We will use property of triangles to find it, that sum of all interior angle of a triangle is equal to 1800{180^0}
⇒∠ABC+∠ACB+∠BAC=1800 ⇒1200+150+∠BAC=1800 ⇒∠BAC=1800−1200−150 ⇒∠BAC=450  \Rightarrow \angle ABC + \angle ACB + \angle BAC = {180^0} \\\ \Rightarrow {120^0} + {15^0} + \angle BAC = {180^0} \\\ \Rightarrow \angle BAC = {180^0} - {120^0} - {15^0} \\\ \Rightarrow \angle BAC = {45^0} \\\
Now applying sine rule,
ACsin⁡∠ABC=BCsin⁡∠BAC ⇒8x−3sin⁡1200=4x−1sin⁡450 ⇒8x−332=4x−112 ⇒(8x−3)23=(4x−1)21 ⇒16x−6=(4x−1)6 ⇒16x−46x=−6+6 ⇒4x(4−6)=6−6 ⇒x=6−64(4−6)  \dfrac{{AC}}{{\sin \angle ABC}} = \dfrac{{BC}}{{\sin \angle BAC}} \\\ \Rightarrow \dfrac{{8x - 3}}{{\sin {{120}^0}}} = \dfrac{{4x - 1}}{{\sin {{45}^0}}} \\\ \Rightarrow \dfrac{{8x - 3}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{4x - 1}}{{\dfrac{1}{{\sqrt 2 }}}} \\\ \Rightarrow \dfrac{{(8x - 3)2}}{{\sqrt 3 }} = \dfrac{{(4x - 1)\sqrt 2 }}{1} \\\ \Rightarrow 16x - 6 = (4x - 1)\sqrt 6 \\\ \Rightarrow 16x - 4\sqrt 6 x = - \sqrt 6 + 6 \\\ \Rightarrow 4x\left( {4 - \sqrt 6 } \right) = 6 - \sqrt 6 \\\ \Rightarrow x = \dfrac{{6 - \sqrt 6 }}{{4\left( {4 - \sqrt 6 } \right)}} \\\
Rationalizing the it by multiplying and dividing with (4+6)\left( {4 + \sqrt 6 } \right)
⇒x=6−64(4−6)×(4+6)(4+6) ⇒x=(6−6)(4+6)4(42−(6)2)  \Rightarrow x = \dfrac{{6 - \sqrt 6 }}{{4\left( {4 - \sqrt 6 } \right)}} \times \dfrac{{\left( {4 + \sqrt 6 } \right)}}{{\left( {4 + \sqrt 6 } \right)}} \\\ \Rightarrow x = \dfrac{{\left( {6 - \sqrt 6 } \right)\left( {4 + \sqrt 6 } \right)}}{{4\left( {{4^2} - {{\left({\sqrt 6 } \right)}^2}} \right)}} \\\
Simplifying it further, we will get
⇒x=(24−46+66−6)4(16−6) ⇒x=(18+26)4(10) ⇒x=2(9+6)4(10) ⇒x=9+620  \Rightarrow x = \dfrac{{\left( {24 - 4\sqrt 6 + 6\sqrt 6 - 6} \right)}}{{4\left( {16 - 6} \right)}} \\\ \Rightarrow x = \dfrac{{\left( {18 + 2\sqrt 6 } \right)}}{{4\left( {10} \right)}} \\\ \Rightarrow x = \dfrac{{2\left( {9 + \sqrt 6 } \right)}}{{4\left( {10} \right)}} \\\ \Rightarrow x = \dfrac{{9 + \sqrt 6 }}{{20}} \\\
So we have proved the value of x=9+620x = \dfrac{{9 + \sqrt 6 }}{{20}}

Note: We have calculated the angle instead of the side of the triangle for second pair of angle and side, because according to this question we have to find the equation of the third side with help of the first two which is much more complex than finding the third angle of a triangle when two of it are given.