Question

Trajectories of two projectiles are shown in figure. Let ${T_1}$ and ${T_2}$ be their time periods and ${u_1}$ and ${u_2}$ their speeds of projection Then:

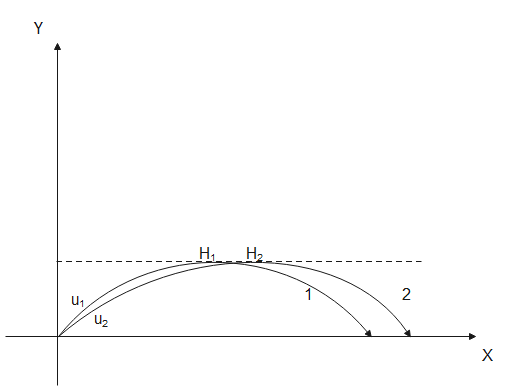
(A) ${T_1} = {T_2}$
(B) ${T_1} > {T_2}$
(C) ${u_1} > {u_2}$
(D) ${u_1} < {u_2}$

Answer 1

This question utilizes the concept of projectile motion. From the figure, we can see that the maximum height in both cases are equal. Thus, we first equate max height of projectile one with max height of projectile two. Then we compare their time periods to get the answer.

Formulae used:
${H_{\max }} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ Where ${H_{\max }}$ is the maximum height attained by the projectile, $u$ is the initial velocity, $\theta$ is the angle of projection and $g$ is the acceleration due to gravity
$T = \dfrac{{2u\sin \theta }}{g}$ Where $T$ is the time of flight of the projectile is, $u$ is the initial velocity, $\theta$ is the angle of projection and $g$ is the acceleration due to gravity

Complete step by step answer:
Let projectile $1$ have max height ${H_1}$ , Time of flight ${T_1}$ , angle of projection ${\theta _1}$ and initial velocity ${u_1}$
Let projectile $2$ have max height ${H_2}$ , Time of flight ${T_2}$ , angle of projection ${\theta _2}$ and initial velocity ${u_2}$

From the figure, we can see that
${H_1} = {H_2}$
Putting in the equation of maximum height, we get
$\Rightarrow \dfrac{{u_1^2{{\sin }^2}{\theta _1}}}{{2g}} = \dfrac{{u_2^2{{\sin }^2}{\theta _2}}}{{2g}}$
$\Rightarrow u_1^2{\sin ^2}{\theta _1} = u_2^2{\sin ^2}{\theta _2}$
$\Rightarrow {\left( {{u_1}\sin {\theta _1}} \right)^2} = {\left( {{u_2}\sin {\theta _2}} \right)^2}$
Putting square root on both the sides, we get

$\Rightarrow {u_1}\sin {\theta _1} = {u_2}\sin {\theta _2}$ ------------(i)
Now, dividing ${T_1}$ by ${T_2}$ , we get
$\Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\dfrac{{2{u_1}\sin {\theta _1}}}{g}}}{{\dfrac{{2{u_2}\sin {\theta _2}}}{g}}} \\\ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{{u_1}\sin {\theta _1}}}{{{u_2}\sin {\theta _2}}} \\\$
Substituting the value of ${u_1}\sin {\theta _1}$ from equation (i), we get
$\Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{{u_2}\sin {\theta _2}}}{{{u_2}\sin {\theta _2}}} \\\ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = 1 \\\$
$\Rightarrow {T_1} = {T_2}$
Therefore, the correct option is (A) ${T_1} = {T_2}$.

Note: Here, we are reminded of the unique property of projectile motion that when the maximum height attained by two particles is the same, the time of flight will always be equal. This is because the time of flight is only dependent on the movement of the projectile in the $y$ axis. This property can be kept in mind for faster solving of questions.