Question

Trace the following central conics. $2{{\left( 3x-4y+5 \right)}^{2}}-3{{\left( 4x+3y-10 \right)}^{2}}=150$.

Answer 1

Hint: We will do some basic operation in the given quadratic equation to form the equation like the standard equation of any conics and then compare the obtained equation with the standard equation of the conic to get the points.

Complete step-by-step solution -
It is given in the question to trace the central conics $2{{\left( 3x-4y+5 \right)}^{2}}-3{{\left( 4x+3y-10 \right)}^{2}}=150$. So, basically central conics means that it will be either a hyperbola or an ellipse. Now, we have given equation of central conic is $2{{\left( 3x-4y+5 \right)}^{2}}-3{{\left( 4x+3y-10 \right)}^{2}}=150$.
On multiplying and dividing 25 to both terms in the LHS we get -
$\Rightarrow 2\times 25\times {{\left( \dfrac{3x-4y+5}{5} \right)}^{2}}-3\times 25\times {{\left( \dfrac{4x+3y-10}{5} \right)}^{2}}=150$, that is, $\Rightarrow 50{{\left( \dfrac{3x-4y+5}{5} \right)}^{2}}-75{{\left( \dfrac{4x+3y-10}{5} \right)}^{2}}=150$
on dividing both sides with 150, we get
$\Rightarrow \dfrac{50{{\left( \dfrac{3x-4y+5}{5} \right)}^{2}}}{150}-\dfrac{75{{\left( \dfrac{4x+3y-10}{5} \right)}^{2}}}{150}=\dfrac{150}{150}$
on solving we get
$\Rightarrow \dfrac{{{\left( \dfrac{3x-4y+5}{5} \right)}^{2}}}{3}-\dfrac{{{\left( \dfrac{4x+3y-10}{5} \right)}^{2}}}{2}=1$.
In order to simplify the solution further, let us assume $X=\left( \dfrac{3x-4y+5}{5} \right)$ and $Y=\left( \dfrac{4x+3y-10}{5} \right)$ . Then we have the equation in reduced form as $\dfrac{{{X}^{2}}}{3}-\dfrac{{{Y}^{2}}}{2}=1......(i)$.
Now, we know that standard equation of hyperbola is $\dfrac{{{X}^{2}}}{{{a}^{2}}}-\dfrac{{{Y}^{2}}}{{{b}^{2}}}=1$.
So, on comparing equation (i) with the standard equation of hyperbola, we get ${{a}^{2}}=3$ so $a=\sqrt{3}$, similarly ${{b}^{2}}=2$ so $b=\sqrt{2}$.
Thus we get $a=\sqrt{3}$ and $b=\sqrt{2}$.
We can trace the hyperbola as:

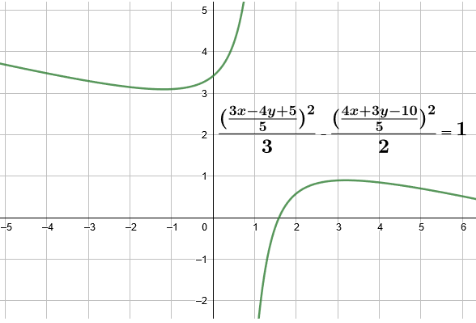
Note: Usually students get confused why we have compared equation (i) with standard equation of hyperbola but not with standard equation of ellipse. This is because we have negative ‘-‘ sign in between the two terms on the left hand side, which is the same as in the standard equation of hyperbola, thus we will consider hyperbola standard equation and not ellipse standard equation.