Question

Trace the curve $y={{x}^{3}}$.

Answer 1

Hint: To trace a graph, first check its domain and range. Then find its intercepts with the coordinate axes. Net check for symmetry and if the curve is asymptotic or not. Next check its derivative to find its increasing or decreasing nature. Finally, find its second derivative to check for any points of inflection.

Complete step-by-step answer:
We have to trace the curve $y={{x}^{3}}$ .
We will first check its domain and range. Since $x$ and $y$ are real numbers, we have
$x\in \mathbb{R}$ and $y\in \mathbb{R}$, the domain and range both stretch over all real numbers.
Now we will find the intercepts with the coordinate axes.
When $x=0$, we get $y=0$.
When $y=0$, we get $x=0$.
$\begin{aligned} & y={{x}^{3}} \\\ & x=0 \\\ & y=0 \\\ \end{aligned}$
This means that the curve passes through the origin.
Now, let us check its symmetry.
Substitute x by -x , we will get ${{y}_{1}}=-{{x}^{3}}=-y$
So $y={{x}^{3}}$ satisfies the property that $f\left( -x \right)=-f\left( x \right)$ .
So it is an odd function and is symmetric about the origin.
Now let us check if the function is asymptotic or not.
When $x\to \infty ,y\to \infty$ and vice versa.
So the function is not asymptotic.
Now, let us check its derivative:
$\dfrac{dy}{dx}=3{{x}^{2}}$
Since $3{{x}^{2}}>0\forall x$
Hence, $\dfrac{dy}{dx}>0\forall x$
Hence, the graph is monotonically increasing and will intersect the axes at the origin only.
Now, let us check its second derivative:
$\dfrac{{{d}^{2}}y}{d{{x}^{2}}}=6x$
$6x=0$ for $x=0$ . At $x=0$, we have $y=0$ .
So, $\left( 0,0 \right)$ is the point of inflection.
Using all this information, we draw the following graph:

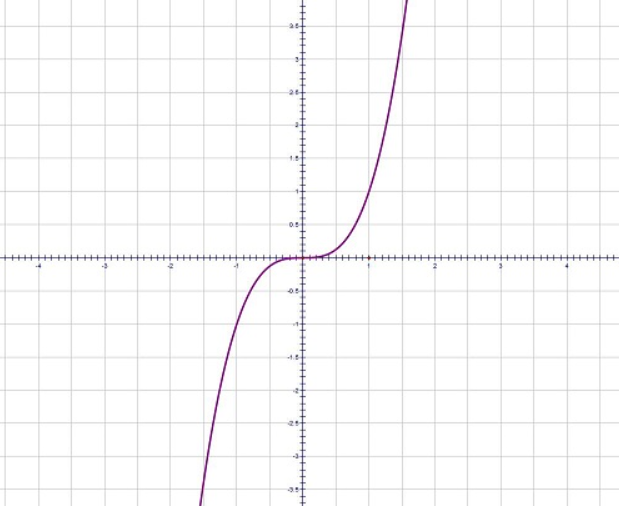
Note: Notice that when $x>0,y>0$ and when $x<0,y<0$ . So the curve will lie only in the quadrants 1 and 3. We can also find the intervals where $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}>0$ or $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}<0$ to check for the nature of curvature in the interval.