Solveeit Logo
Login

Question

Question: The exact value of $\frac{96 \sin 80^\circ \sin 65^\circ \sin 35^\circ}{\sin 20^\circ + \sin 50^\cir...

The exact value of 96sin⁡80∘sin⁡65∘sin⁡35∘sin⁡20∘+sin⁡50∘+sin⁡110∘\frac{96 \sin 80^\circ \sin 65^\circ \sin 35^\circ}{\sin 20^\circ + \sin 50^\circ + \sin110^\circ} is equal to

A

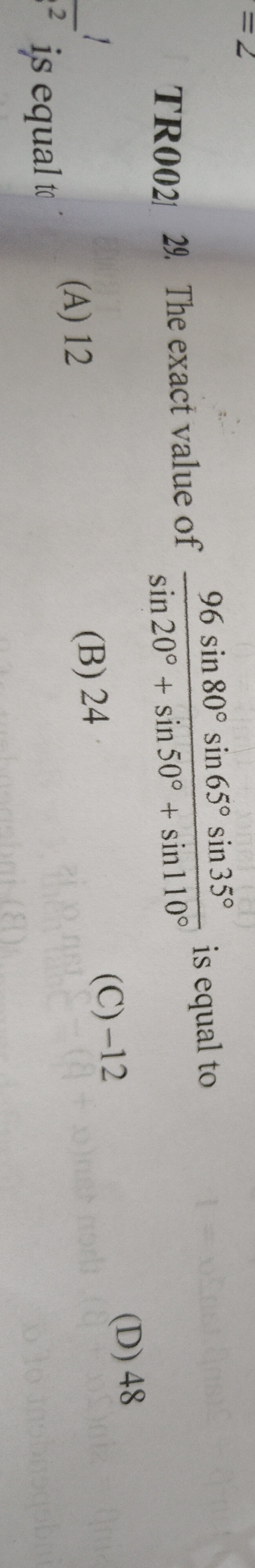
12

B

24

C

-12

D

48

Answer

24

Explanation

Solution

Explanation of the Solution:

The problem asks for the exact value of the trigonometric expression 96sin⁡80∘sin⁡65∘sin⁡35∘sin⁡20∘+sin⁡50∘+sin⁡110∘\frac{96 \sin 80^\circ \sin 65^\circ \sin 35^\circ}{\sin 20^\circ + \sin 50^\circ + \sin110^\circ}.

  1. Simplify the Numerator:

Let the numerator be N=96sin⁡80∘sin⁡65∘sin⁡35∘N = 96 \sin 80^\circ \sin 65^\circ \sin 35^\circ. Using the complementary angle identity sin⁡x=cos⁡(90∘−x)\sin x = \cos(90^\circ - x):

  • sin⁡80∘=cos⁡(90∘−80∘)=cos⁡10∘\sin 80^\circ = \cos(90^\circ - 80^\circ) = \cos 10^\circ
  • sin⁡65∘=cos⁡(90∘−65∘)=cos⁡25∘\sin 65^\circ = \cos(90^\circ - 65^\circ) = \cos 25^\circ
  • sin⁡35∘=cos⁡(90∘−35∘)=cos⁡55∘\sin 35^\circ = \cos(90^\circ - 35^\circ) = \cos 55^\circ

So, the numerator becomes N=96cos⁡10∘cos⁡25∘cos⁡55∘N = 96 \cos 10^\circ \cos 25^\circ \cos 55^\circ.

  1. Simplify the Denominator:

Let the denominator be D=sin⁡20∘+sin⁡50∘+sin⁡110∘D = \sin 20^\circ + \sin 50^\circ + \sin 110^\circ. First, check the sum of the angles: 20∘+50∘+110∘=180∘20^\circ + 50^\circ + 110^\circ = 180^\circ. For angles A,B,CA, B, C such that A+B+C=180∘A+B+C = 180^\circ, the following identity holds: sin⁡A+sin⁡B+sin⁡C=4cos⁡(A2)cos⁡(B2)cos⁡(C2)\sin A + \sin B + \sin C = 4 \cos\left(\frac{A}{2}\right) \cos\left(\frac{B}{2}\right) \cos\left(\frac{C}{2}\right). Applying this identity with A=20∘A=20^\circ, B=50∘B=50^\circ, C=110∘C=110^\circ:

  • A2=20∘2=10∘\frac{A}{2} = \frac{20^\circ}{2} = 10^\circ
  • B2=50∘2=25∘\frac{B}{2} = \frac{50^\circ}{2} = 25^\circ
  • C2=110∘2=55∘\frac{C}{2} = \frac{110^\circ}{2} = 55^\circ

So, the denominator becomes D=4cos⁡10∘cos⁡25∘cos⁡55∘D = 4 \cos 10^\circ \cos 25^\circ \cos 55^\circ.

  1. Calculate the Ratio:

Now, substitute the simplified numerator and denominator back into the original expression: 96sin⁡80∘sin⁡65∘sin⁡35∘sin⁡20∘+sin⁡50∘+sin⁡110∘=96cos⁡10∘cos⁡25∘cos⁡55∘4cos⁡10∘cos⁡25∘cos⁡55∘\frac{96 \sin 80^\circ \sin 65^\circ \sin 35^\circ}{\sin 20^\circ + \sin 50^\circ + \sin110^\circ} = \frac{96 \cos 10^\circ \cos 25^\circ \cos 55^\circ}{4 \cos 10^\circ \cos 25^\circ \cos 55^\circ} Since 10∘,25∘,55∘10^\circ, 25^\circ, 55^\circ are acute angles, their cosines are non-zero. We can cancel the common term cos⁡10∘cos⁡25∘cos⁡55∘\cos 10^\circ \cos 25^\circ \cos 55^\circ from the numerator and the denominator. =964=24= \frac{96}{4} = 24

The exact value of the expression is 24.