Solveeit Logo
Login

Question

Question: To find the number of solutions of the equation \(\sin \theta +\cos \theta =\sin 2\theta \) in the i...

To find the number of solutions of the equation sin⁡θ+cos⁡θ=sin⁡2θ\sin \theta +\cos \theta =\sin 2\theta in the interval [π,−π][\pi ,-\pi ]-
(a) 1
(b) 2
(c) 3
(d) 4

Explanation

Solution

Hint: Since, we have different terms (in terms that on LHS, there are trigonometric terms containing θ\theta and on RHS, there is a 2θ2\theta term) on LHS and RHS of the trigonometric equation, we solve this trigonometric equation by squaring LHS and RHS terms. This way we will be able to simplify the equation easily.

Complete step-by-step answer:
Thus, we have,
sin⁡θ+cos⁡θ=sin⁡2θ\sin \theta +\cos \theta =\sin 2\theta
Now, squaring the LHS and RHS, we have,
(sin⁡θ+cos⁡θ)2=(sin⁡2θ)2{{(\sin \theta +\cos \theta )}^{2}}={{(\sin 2\theta )}^{2}}
(sin⁡θ)2+(cos⁡θ)2+2sin⁡θcos⁡θ=(sin⁡2θ)2{{(\sin \theta )}^{2}}+{{(\cos \theta )}^{2}}+2\sin \theta \cos \theta ={{(\sin 2\theta )}^{2}}
1+sin⁡2θ=(sin⁡2θ)2\sin 2\theta ={{(\sin 2\theta )}^{2}} -- (1)
Since, (sin⁡θ)2+(cos⁡θ)2=1{{(\sin \theta )}^{2}}+{{(\cos \theta )}^{2}}=1 and 2sin⁡θcos⁡θ=sin⁡2θ2\sin \theta \cos \theta =\sin 2\theta
Now, solving (1) further,
1+sin⁡2θ=(sin⁡2θ)2\sin 2\theta ={{(\sin 2\theta )}^{2}}
Let sin⁡2θ\sin 2\theta =t, thus, we have,
1+t=t2t={{t}^{2}}
t2−t−1=0{{t}^{2}}-t-1=0-- (2)
To solve, ax2+bx+c=0a{{x}^{2}}+bx+c=0, the solution is-
x=−b±b2−4ac2a\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}
Now solving the equation (2), we have,
t= 1±12−4(−1)(1)2(1)\dfrac{1\pm \sqrt{{{1}^{2}}-4(-1)(1)}}{2(1)}
t=1±52\dfrac{1\pm \sqrt{5}}{2}
Now, we can eliminate, t=1+52\dfrac{1+\sqrt{5}}{2}=1.618
Since, t=sin⁡2θ\sin 2\theta would be greater than 1. This would not be possible since, -1≤\le sin⁡2θ\sin 2\theta ≤\le 1.
Thus, we only have one solution,
t=1−52\dfrac{1-\sqrt{5}}{2}
Since, t=sin⁡2θ\sin 2\theta , we have,
sin⁡2θ\sin 2\theta =1−52\dfrac{1-\sqrt{5}}{2}
Now, to solve this equation, we will make use of graph,

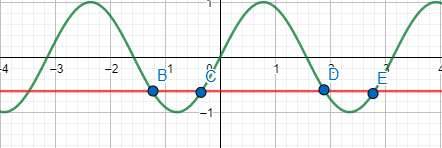
Now, to get the number of solutions, we have to find the number of intersection of y=1−52\dfrac{1-\sqrt{5}}{2}and y=sin⁡2θ\sin 2\theta between [π,−π\pi ,-\pi ]. (Also, for reference, π\pi is approximately 3.14)
Clearly, we see that there are four intersections within the range [π,−π\pi ,-\pi ].
Hence, there are four solutions to the trigonometric equation sin⁡θ+cos⁡θ=sin⁡2θ\sin \theta +\cos \theta =\sin 2\theta .

Note: While solving trigonometric equations, we should try to solve the question by bringing LHS and RHS in same degree of angle (that is, in this case, by squaring the LHS and RHS terms, we were eventually able to bring both LHS and RHS in terms of 2θ2\theta . Finally, we should ensure that the solution is always within the limits [-1,1] since, -1≤\le sin⁡x\sin x ≤\le 1.