Question
Question: To determine the half-life of a radioactive element, the student plots a graph of ln|dN(t)/dt| versu...
To determine the half-life of a radioactive element, the student plots a graph of ln|dN(t)/dt| versus t. Here dN(t)/dt is the rate of radioactive decay at time t. If the number of radioactive nuclei of this element decreases by a factor of p after 4.16 years, the value of p is:
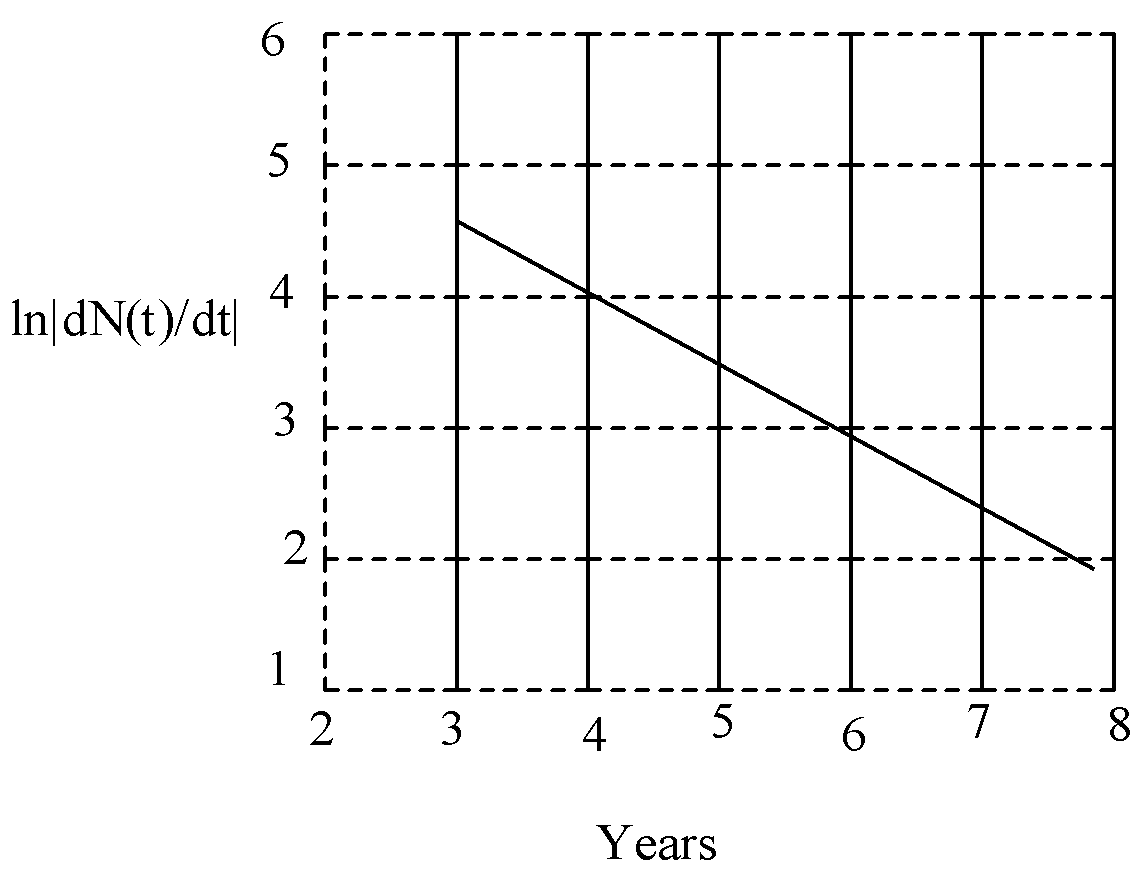
Solution
To calculate the radioactive decay, the equation used is N(t)=N∘e−λt where N is the radioactive nuclei present at time t and N∘ is the number of radioactive nuclei present initially. The half-life of the first-order reaction is calculated by dividing 0.693 to radioactive decay constant.
Complete answer:
The number of nuclei disintegration per second of a radioactive sample at any instant is directly proportional to the number of undecayed nuclei present in the sample at that instant.
The equation which represents the radioactive decay law is:
N(t)=N∘e−λt
dtdN=N∘λe−λt
Where N is the radioactive nuclei present at time t
N∘ is the number of radioactive nuclei present initially.
dN is the number of radioactive nuclei which disintegrate in the small time interval of time dt.
Taking log on both side of the equation, we get
lndtdN=ln(N∘λ−λt)
So, from this equation the slope of the curve, m=−λ
So, from the graph,
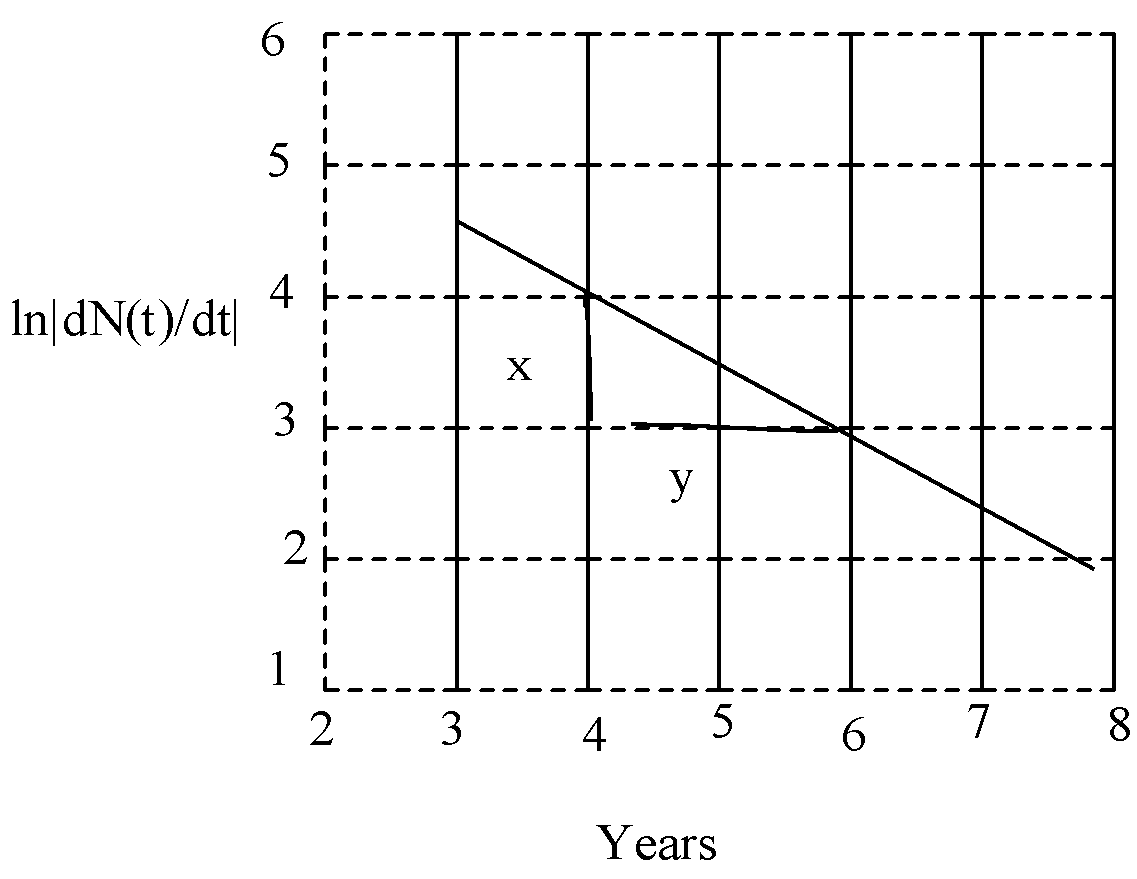
m=ΔxΔy=21=0.5
So, the radioactive decay constant is 0.5.
The half life of first order reaction is calculated by dividing 0.693 to radioactive decay constant.
t1/2=λ0.693
So, putting the values, we get
t1/2=λ0.693=0.50.693=0.3465years
Hence, the half life of the radioactive sample is 0.3465 years.
According to the question,
N(t)=N∘e−λt
p1=e−λt
The time given is 4.16 years.
So, p1=e−0.5 x 4.16
p=8
So, the value of p is 8.
Note: All the formulas must be taken correctly. When converting the equation to log form the negative sign must also be taken. In half-life, the value of log 2 is directly taken 0.693.
