Question
Question: The vectors are $\vec{a} = 2\hat{i} + \hat{j} - 2\hat{k}, \vec{b} = \hat{i} + \hat{j}$ if $\vec{c}$ ...
The vectors are a=2i^+j^−2k^,b=i^+j^ if c is a vector such that a⋅c=∣c∣ and ∣c−a∣=22. Angle between a×b and c is 4π then ∣(a×b)×c∣ is
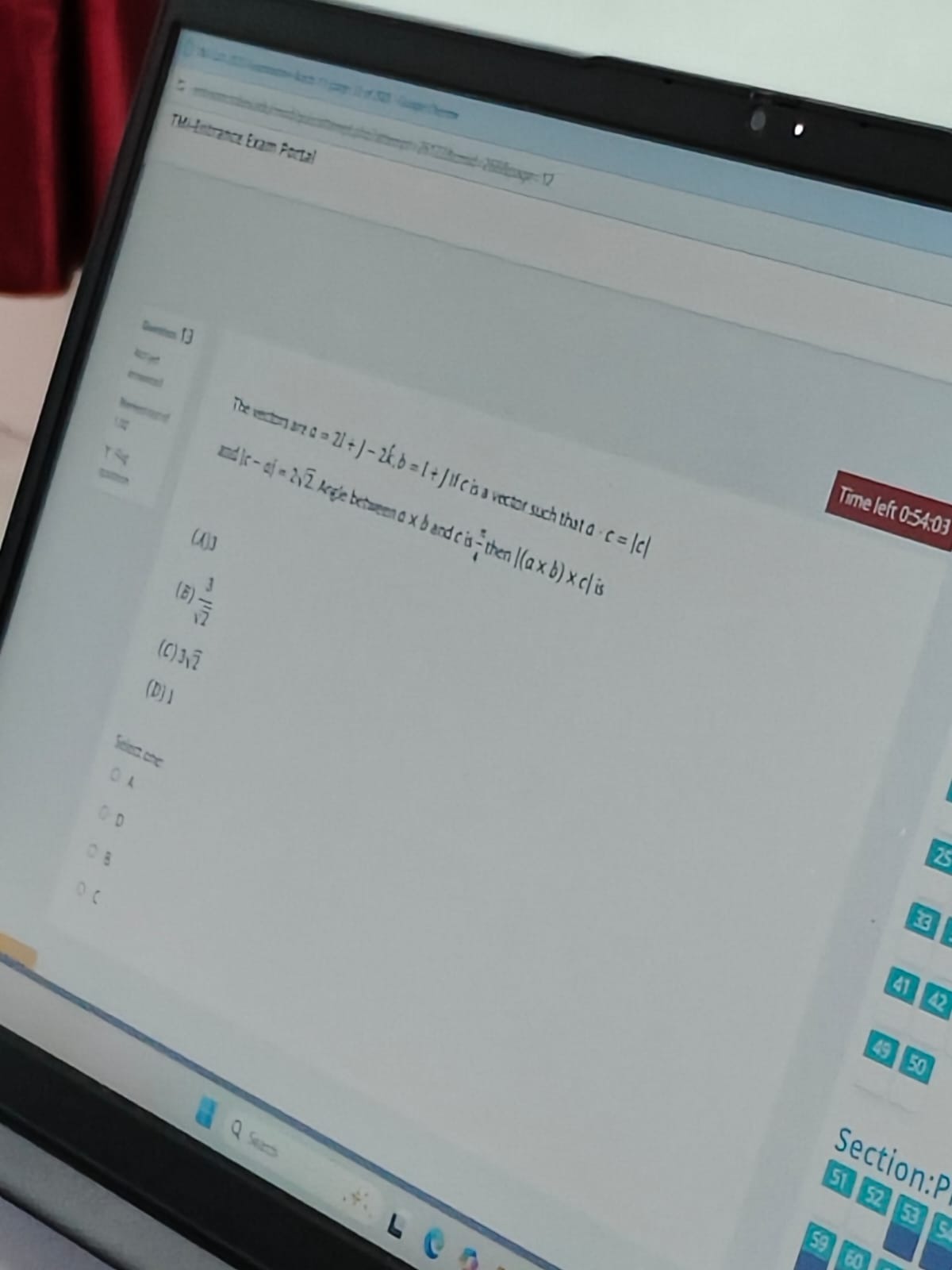
3
23
32
1
23
Solution
To find ∣(a×b)×c∣, we need to calculate the magnitudes of a×b and c, and the sine of the angle between them.
Step 1: Calculate a×b and its magnitude. Given a=2i^+j^−2k^ and b=i^+j^. The cross product a×b is:
a×b=i^21j^11k^−20 =i^((1)(0)−(−2)(1))−j^((2)(0)−(−2)(1))+k^((2)(1)−(1)(1)) =i^(0+2)−j^(0+2)+k^(2−1) =2i^−2j^+k^Let d=a×b. The magnitude of d is:
∣d∣=∣2i^−2j^+k^∣=22+(−2)2+12=4+4+1=9=3Step 2: Find the magnitude of c using the given conditions. We are given two conditions for c:
- a⋅c=∣c∣
- ∣c−a∣=22
First, let's find the magnitude of a:
∣a∣=∣2i^+j^−2k^∣=22+12+(−2)2=4+1+4=9=3Now, square the second condition:
∣c−a∣2=(22)2Using the property ∣x∣2=x⋅x:
(c−a)⋅(c−a)=8 ∣c∣2−2(c⋅a)+∣a∣2=8Substitute the first condition (c⋅a=∣c∣) and the value of ∣a∣=3:
∣c∣2−2∣c∣+32=8 ∣c∣2−2∣c∣+9=8Rearrange the terms to form a quadratic equation in ∣c∣:
∣c∣2−2∣c∣+1=0This is a perfect square trinomial:
(∣c∣−1)2=0Therefore,
∣c∣=1Step 3: Calculate ∣(a×b)×c∣. We need to find ∣d×c∣. The magnitude of the cross product of two vectors is given by ∣X×Y∣=∣X∣∣Y∣sinθ, where θ is the angle between X and Y. Here, X=d=a×b and Y=c. We found ∣d∣=3 and ∣c∣=1. The angle between a×b and c is given as 4π. So, θ=4π.
∣(a×b)×c∣=∣d∣∣c∣sin(4π) =(3)(1)(21) =23