Question

Tick the correct answer in the following, Area of sector of angle $\theta$ ( in degrees ) of a circle with radius R is,
( a ) $\dfrac{\theta }{180}\times 2\pi R$
( b ) $\dfrac{\theta }{180}\times \pi {{R}^{2}}$
( c ) $\dfrac{\theta }{3600}\times 2\pi R$
( d ) $\dfrac{\theta }{720}\times 2\pi {{R}^{2}}$

Answer 1

In the question, we are asked to find the formula of area of sector of a circle in degree.
Now, what we can do is we can just re arrange the option provided in question and can compare it with the formula of area of sector of circle and degree and we will eliminate the wrong options until we get the right option.

Complete step by step answer:
Let, we have a circle of radius R with center O. Then the area of the circle is equal to ${{A}_{C}}=\pi {{R}^{2}}$ .

Now, first we see what is meant by sector of circle.
Sector of a circle is the portion of a circle enclosed by two radii and an arc, where the smaller area is called minor sector and larger area is called major sector.
In figure, OB and OA are two radii and O is the centre of the circle and AB is an arc, then OAB represents the sector of the circle.

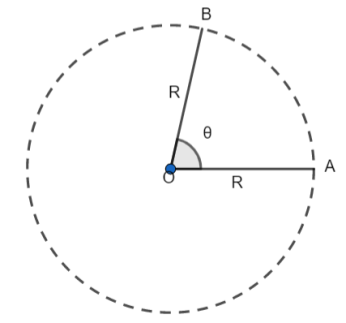
If, $\theta$ is the angle subtended by the sector of circle, then the area of sector is equals to
${{A}_{S}}=\dfrac{\theta }{{{360}^{{}^\circ }}}\times \pi {{R}^{2}}$………( i ) , where R is radius of circle, $\theta$ is the angle subtended by the sector of circle and $\pi =\dfrac{22}{7}$ or $\pi =3.14$
Now, from options,
Option ( a ) is not equal to equation ( i ), as ${{R}^{2}}$ is missing.
Option ( b ) is not equal to equation ( i ), as the angle given is 180 not 360.
Option ( c ) is not equal to equation ( i ), as angle is 3600 instead of 360 and ${{R}^{2}}$is missing.
Now, option ( d ) can be re – written as,
$\dfrac{\theta }{720}\times 2\pi {{R}^{2}}=\dfrac{\theta }{360}\times \pi {{R}^{2}}$, which is equals to equation ( i ).
Hence, option ( d ) is correct.

Note:
To solve such questions where there is no calculation, the knowledge of important formulae come in use, so one must know all the formulas and theorems related to circles, semicircles, sectors and segments. Also, try to re – write the options in the form of given equations as it helps in solving questions faster.