Question
Question: PT $\frac{Sin 7\theta - Sin 5\theta}{Cos 7\theta + Cos 5\theta}$ = Tan$\theta$...
PT Cos7θ+Cos5θSin7θ−Sin5θ = Tanθ
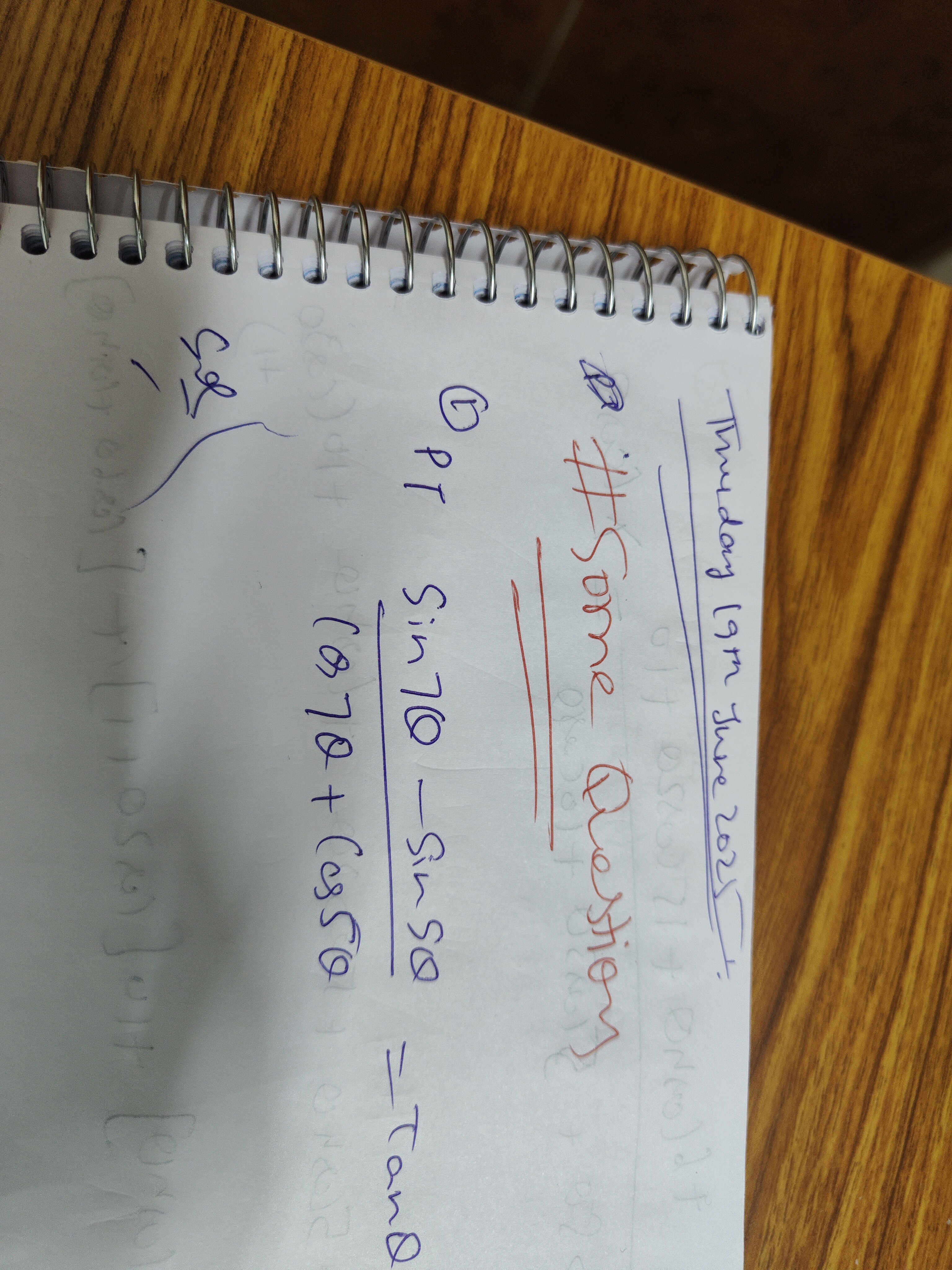
Proven
Solution
To prove the identity cos7θ+cos5θsin7θ−sin5θ=tanθ, we will use the sum-to-product trigonometric formulas.
The relevant formulas are:
- sinA−sinB=2cos(2A+B)sin(2A−B)
- cosA+cosB=2cos(2A+B)cos(2A−B)
Let's apply these to the Left Hand Side (LHS) of the given identity. For the numerator, sin7θ−sin5θ: Here, A=7θ and B=5θ. 2A+B=27θ+5θ=212θ=6θ 2A−B=27θ−5θ=22θ=θ So, the numerator becomes:
sin7θ−sin5θ=2cos6θsinθFor the denominator, cos7θ+cos5θ: Here, A=7θ and B=5θ. 2A+B=27θ+5θ=212θ=6θ 2A−B=27θ−5θ=22θ=θ So, the denominator becomes:
cos7θ+cos5θ=2cos6θcosθNow, substitute these expressions back into the LHS:
LHS=2cos6θcosθ2cos6θsinθAssuming cos6θ=0, we can cancel out the common terms (2cos6θ):
LHS=cosθsinθWe know that cosθsinθ=tanθ.
LHS=tanθThis is equal to the Right Hand Side (RHS) of the given identity. Hence, the identity is proven.
Explanation of the solution: The identity is proven by applying sum-to-product formulas for sine and cosine to the numerator and denominator respectively. The common term 2cos6θ cancels out, simplifying the expression to cosθsinθ, which is tanθ.
