Question

Through the vertex A of the parabola ${{y}^{2}}=4ax$ two chords AP and AQ are drawn, and the circles on AP and AQ as diameters intersect in R. Prove that, if ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\phi$ be the angles made with the axis by the tangents at P and Q and by AR, then prove that $\cot {{\theta }_{1}}+\cot {{\theta }_{2}}+\tan \phi =0$?

Answer 1

We start solving the problem by drawing all the given information and recalling the concept of vertex and parametric points of parabola ${{y}^{2}}=4ax$. We then assume the parametric points for P, Q and we find the center and equation of the circles with AP and AQ as diameter. We then find the equation of the common chord of two circles by subtracting the equation. We then find the slope of the common chord and recall the formula of the slope. Similarly, we use the definition of tangent at the point on a parabola for points P and Q and find the value $\cot {{\theta }_{1}},\cot {{\theta }_{2}}$. We then add all the results obtained to complete the proof.

Complete step by step answer:
According to the problem, we have a parabola ${{y}^{2}}=4ax$ with vertex at A and two chords AP and AQ are drawn. Circles are drawn by taking AP and AQ as diameters which intersect at R. We need to prove$\cot {{\theta }_{1}}+\cot {{\theta }_{2}}+2\tan \phi =0$, where ${{\theta }_{1}}$, ${{\theta }_{2}}$ and $\phi$ be the angles made with the axis by the tangents at P and Q and by AR.

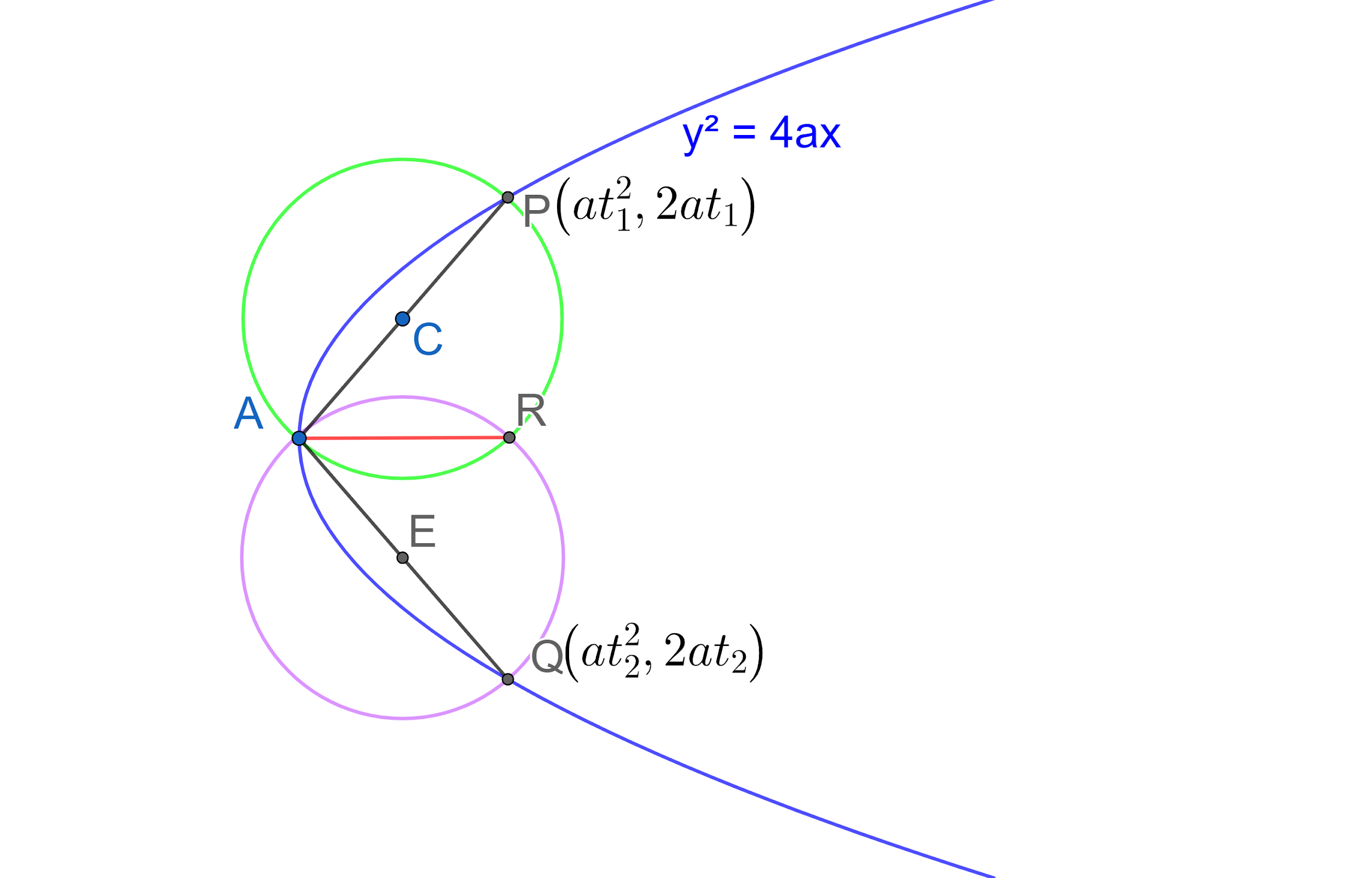
We know that the vertex of the parabola ${{y}^{2}}=4ax$ is $\left( 0,0 \right)$. So, we have got the co-ordinates of point A as $A\left( 0,0 \right)$. We know that the parametric equation of the point that lies on the parabola is $\left( a{{t}^{2}},2at \right)$. So, let us assume the points P and Q be $\left( at_{1}^{2},2a{{t}_{1}} \right)$, $\left( at_{2}^{2},2a{{t}_{2}} \right)$.
Let us find the center of the circle with AP as diameter. Let us assume the center be C.
$\Rightarrow C=\left( \dfrac{0+at_{1}^{2}}{2},\dfrac{0+2a{{t}_{1}}}{2} \right)$.
$\Rightarrow C=\left( \dfrac{at_{1}^{2}}{2},\dfrac{2a{{t}_{1}}}{2} \right)$.
$\Rightarrow C=\left( \dfrac{at_{1}^{2}}{2},a{{t}_{1}} \right)$.
We know that equation of the circle with center $(a,b)$ and passing through the point $\left( c,d \right)$ is ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{\left( c-a \right)}^{2}}+{{\left( d-b \right)}^{2}}$.
The equation of the circle with center $C\left( \dfrac{at_{1}^{2}}{2},a{{t}_{1}} \right)$ and passing through $A\left( 0,0 \right)$ is ${{\left( x-\dfrac{at_{1}^{2}}{2} \right)}^{2}}+{{\left( y-a{{t}_{1}} \right)}^{2}}={{\left( 0-\dfrac{at_{1}^{2}}{2} \right)}^{2}}+{{\left( 0-a{{t}_{1}} \right)}^{2}}$.
$\Rightarrow {{x}^{2}}-xat_{1}^{2}+\dfrac{{{a}^{2}}t_{1}^{4}}{4}+{{y}^{2}}-2a{{t}_{1}}y+{{a}^{2}}t_{1}^{2}=\dfrac{{{a}^{2}}t_{1}^{4}}{4}+{{a}^{2}}t_{1}^{2}$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}-at_{1}^{2}x-2a{{t}_{1}}y=0$ ---(1).
Let us find the center of the circle with AQ as diameter. Let us assume the center be E.
$\Rightarrow E=\left( \dfrac{0+at_{2}^{2}}{2},\dfrac{0+2a{{t}_{2}}}{2} \right)$.
$\Rightarrow E=\left( \dfrac{at_{2}^{2}}{2},\dfrac{2a{{t}_{2}}}{2} \right)$.
$\Rightarrow E=\left( \dfrac{at_{2}^{2}}{2},a{{t}_{2}} \right)$.
The equation of the circle with center $E\left( \dfrac{at_{2}^{2}}{2},a{{t}_{2}} \right)$ and passing through $A\left( 0,0 \right)$ is ${{\left( x-\dfrac{at_{2}^{2}}{2} \right)}^{2}}+{{\left( y-a{{t}_{2}} \right)}^{2}}={{\left( 0-\dfrac{at_{2}^{2}}{2} \right)}^{2}}+{{\left( 0-a{{t}_{2}} \right)}^{2}}$.
$\Rightarrow {{x}^{2}}-xat_{2}^{2}+\dfrac{{{a}^{2}}t_{2}^{4}}{4}+{{y}^{2}}-2a{{t}_{2}}y+{{a}^{2}}t_{2}^{2}=\dfrac{{{a}^{2}}t_{2}^{4}}{4}+{{a}^{2}}t_{2}^{2}$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}-at_{2}^{2}x-2a{{t}_{2}}y=0$ ---(2).
According to the problem, the circles in equation (1) and (2) intersect at point R. Which means that the both circles have a common chord AR. We know that we can find the equation of a common chord by subtracting two circles.
The equation of the common chord of both circles is ${{x}^{2}}+{{y}^{2}}-at_{2}^{2}x-2a{{t}_{2}}y-\left( {{x}^{2}}+{{y}^{2}}-at_{1}^{2}x-2a{{t}_{1}}y \right)=0$.
$\Rightarrow {{x}^{2}}+{{y}^{2}}-at_{2}^{2}x-2a{{t}_{2}}y-{{x}^{2}}-{{y}^{2}}+at_{1}^{2}x+2a{{t}_{1}}y=0$.
$\Rightarrow \left( at_{1}^{2}-at_{2}^{2} \right)x+\left( 2a{{t}_{1}}-2a{{t}_{2}} \right)y=0$.
$\Rightarrow \left( 2a{{t}_{1}}-2a{{t}_{2}} \right)y=-\left( at_{1}^{2}-at_{2}^{2} \right)x$.
$\Rightarrow y=\dfrac{-\left( at_{1}^{2}-at_{2}^{2} \right)}{\left( 2a{{t}_{1}}-2a{{t}_{2}} \right)}x$
$\Rightarrow y=\dfrac{-a\left( {{t}_{1}}-{{t}_{2}} \right)\left( {{t}_{1}}+{{t}_{2}} \right)}{2a\left( {{t}_{1}}-{{t}_{2}} \right)}x$.
$\Rightarrow y=\dfrac{-\left( {{t}_{1}}+{{t}_{2}} \right)}{2}x$ ---(3).
We compare equation (3) with standard slope form of line $y=mx+c$. We get slope $m=\dfrac{-\left( {{t}_{1}}+{{t}_{2}} \right)}{2}$.
We know that slope is calculated by taking the tangent of the angle made by the line with x-axis. According to the problem, we have given that the chord AR makes an angle $\phi$ with x-axis.
So, we have $m=\tan \phi$.
$\Rightarrow \tan \phi =\dfrac{-\left( {{t}_{1}}+{{t}_{2}} \right)}{2}$.
$\Rightarrow 2\tan \phi =-\left( {{t}_{1}}+{{t}_{2}} \right)$ ---(4).
We know that equation of the tangent at the point $\left( a{{t}^{2}},2at \right)$ to the parabola ${{y}^{2}}=4ax$ is $y=\dfrac{x}{t}+at$.
So, we get the equation of tangent at $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ as $y=\dfrac{x}{{{t}_{1}}}+a{{t}_{1}}$ ---(5).
We compare equation (5) with standard slope form of line $y=mx+c$. We get slope ${{m}_{1}}=\dfrac{1}{{{t}_{1}}}$.
We know that slope is calculated by taking the tangent of the angle made by the line with x-axis. According to the problem, we have given that the diameter AP makes an angle ${{\theta }_{1}}$ with x-axis.
So, we have ${{m}_{1}}=\tan {{\theta }_{1}}$.
$\Rightarrow \tan {{\theta }_{1}}=\dfrac{1}{{{t}_{1}}}$.
$\Rightarrow \cot {{\theta }_{1}}={{t}_{1}}$ ---(6).
Similarly, we get the equation of tangent at $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ as $y=\dfrac{x}{{{t}_{2}}}+a{{t}_{2}}$ ---(7).
We compare equation (6) with standard slope form of line $y=mx+c$. We get slope ${{m}_{2}}=\dfrac{1}{{{t}_{2}}}$.
We know that slope is calculated by taking the tangent of the angle made by the line with x-axis. According to the problem, we have given that the diameter AQ makes an angle ${{\theta }_{2}}$ with x-axis.
So, we have ${{m}_{2}}=\tan {{\theta }_{2}}$.
$\Rightarrow \tan {{\theta }_{2}}=\dfrac{1}{{{t}_{2}}}$.
$\Rightarrow \cot {{\theta }_{2}}={{t}_{2}}$---(8).
Now, we consider $\cot {{\theta }_{1}}+\cot {{\theta }_{2}}+2\tan \phi$
$\Rightarrow \cot {{\theta }_{1}}+\cot {{\theta }_{2}}+2\tan \phi ={{t}_{1}}+{{t}_{2}}-\left( {{t}_{1}}+{{t}_{2}} \right)$.
$\Rightarrow \cot {{\theta }_{1}}+\cot {{\theta }_{2}}+2\tan \phi ={{t}_{1}}+{{t}_{2}}-{{t}_{1}}-{{t}_{2}}$.
$\Rightarrow \cot {{\theta }_{1}}+\cot {{\theta }_{2}}+2\tan \phi =0$.

We have proved $\cot {{\theta }_{1}}+\cot {{\theta }_{2}}+2\tan \phi =0$.

Note: We can also find the slope of the tangent of the parabola at a given by taking differentiation of the curve and substituting the given point. We should know that the slope of the line is found by taking the tangent of the angle made by the line with x-axis. In the problem it is not clearly mentioned about the axes that line makes an angle with, in such cases we always take x-axis.