Question

Through the positive vertex of a hyperbola a tangent is drawn; where does it meet the conjugate hyperbola?

Answer 1

We here will first assume the hyperbola to be ${{H}_{1}}$ given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Then, we will calculate its conjugate by either reversing the signs of the coefficients of ${{x}^{2}}$ and ${{y}^{2}}$or by multiplying LHS or RHS by ‘-1’ and name it ${{H}_{2}}$. Then we will draw the figure of this hyperbola along with its tangent and calculate its positive vertex. Then we will calculate the tangent at that point given as:
The tangent at any point $\left( h,k \right)$ on a curve f(x)=y is given as:
$y-k={{\left( \dfrac{dy}{dx} \right)}_{\left( h,k \right)}}\left( x-h \right)$
Then we will solve the each calculated equation of the conjugate hyperbola ${{H}_{2}}$ and hence we will obtain the required points of intersection.

Complete step-by-step solution:
Here we have been given a hyperbola. Let us first assume the hyperbola to be ${{H}_{1}}$ given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Now, we know that in a conjugate hyperbola, the signs of the coefficients of ${{x}^{2}}$ and ${{y}^{2}}$ are reversed, or we can say that either the LHS or the RHS is multiplied by ‘-1’ to obtain the equation of the conjugate hyperbola. Let us assume the conjugate hyperbola to be ${{H}_{2}}$. Hence, ${{H}_{2}}$ is given as:
${{H}_{2}}\equiv \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1$
Now, we will first consider the hyperbola ${{H}_{1}}\equiv \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
We know that in this type of hyperbola, there are two vertices given as ${{V}_{1}}\left( a,0 \right)$ and ${{V}_{2}}\left( -a,0 \right)$. We also know that the respective foci of this hyperbola is given as ${{F}_{1}}\left( ae,0 \right)$ and ${{F}_{2}}\left( -ae,0 \right)$
This hyperbola is shown as follows:

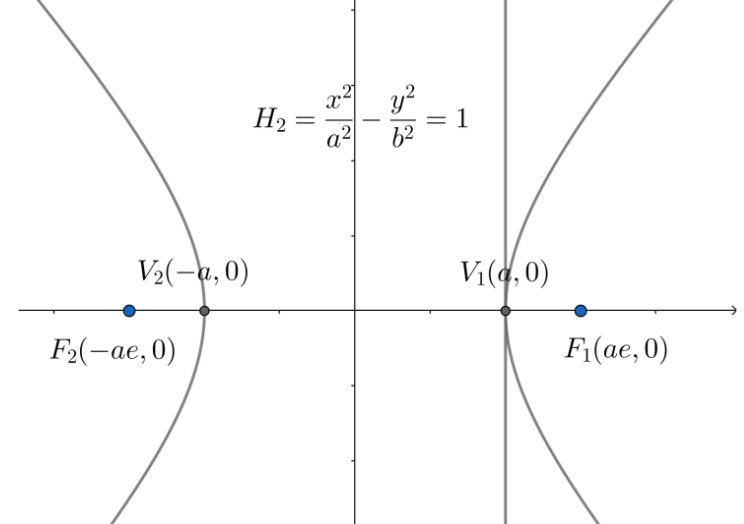
Now, we can see that the positive vertex of this hyperbola is ${{V}_{1}}\left( a,0 \right)$. Now, the tangent on this point is given as follows:
We know that the tangent at any point $\left( h,k \right)$ on a curve f(x)=y is given as:
$y-k={{\left( \dfrac{dy}{dx} \right)}_{\left( h,k \right)}}\left( x-h \right)$
Here, we have the hyperbola as $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Now, the value of $\dfrac{dy}{dx}$ is given as:
$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Differentiating w.r.t. x on both sides we get:
$\begin{aligned} & \dfrac{2x}{{{a}^{2}}}-\dfrac{2y}{{{b}^{2}}}\dfrac{dy}{dx}=0 \\\ & \Rightarrow \dfrac{2x}{{{a}^{2}}}=\dfrac{2y}{{{b}^{2}}}\dfrac{dy}{dx} \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{x}{y}\dfrac{{{b}^{2}}}{{{a}^{2}}} \\\ \end{aligned}$
Now, the value of $\dfrac{dy}{dx}$ at (a,0) is given as:
$\begin{aligned} & \dfrac{dy}{dx}=\dfrac{x}{y}\dfrac{{{b}^{2}}}{{{a}^{2}}} \\\ & \Rightarrow {{\left( \dfrac{dy}{dx} \right)}_{\left( a,0 \right)}}=\dfrac{a}{0}\dfrac{{{b}^{2}}}{{{a}^{2}}} \\\ & \Rightarrow {{\left( \dfrac{dy}{dx} \right)}_{\left( a,0 \right)}}=\dfrac{1}{0} \\\ \end{aligned}$
Thus, the required tangent is given as:
$\begin{aligned} & y-0=\dfrac{1}{0}\left( x-a \right) \\\ & \Rightarrow 0\left( y \right)=1\left( x-a \right) \\\ & \Rightarrow x-a=0 \\\ & \Rightarrow x=a \\\ \end{aligned}$
Now, as mentioned above, the conjugate hyperbola is ${{H}_{2}}\equiv \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1$
We will now solve the tangent with this hyperbola to obtain the required points of intersection.
We here have the tangent as
$x=a$ …..(i)
Now, putting this value of x in ${{H}_{2}}$ and solving we get:
$\begin{aligned} & \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1 \\\ & \Rightarrow \dfrac{{{\left( a \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1 \\\ & \Rightarrow \dfrac{{{a}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1 \\\ & \Rightarrow 1-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1 \\\ & \Rightarrow 2=\dfrac{{{y}^{2}}}{{{b}^{2}}} \\\ & \Rightarrow {{y}^{2}}=2{{b}^{2}} \\\ \end{aligned}$
Now, taking under root on both sides, we get:
$\begin{aligned} & {{y}^{2}}=2{{b}^{2}} \\\ & \Rightarrow y=\pm \sqrt{2}b \\\ \end{aligned}$
Thus, the required points of intersections are $\left( a,\pm \sqrt{2}b \right)$.

Note: We can also obtain the equation of the tangent at a point (h,k) on any curve of degree 2 by using the method of keeping T=0. In this method, the variables with power 2 change as:
$\begin{aligned} & {{x}^{2}}\to h.x \\\ & {{y}^{2}}\to k.y \\\ \end{aligned}$
The variables of power 1 change as:
$\begin{aligned} & x\to \dfrac{1}{2}\left( x+h \right) \\\ & y\to \dfrac{1}{2}\left( y+k \right) \\\ \end{aligned}$
The constants in this method remain the same.
If we find the equation of tangent on ${{H}_{1}}$ by using T=0 at (a,0) we get:
$\begin{aligned} & \dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 \\\ & \Rightarrow \dfrac{a.x}{{{a}^{2}}}-\dfrac{0.y}{{{b}^{2}}}=1 \\\ & \Rightarrow \dfrac{x}{a}-0=1 \\\ & \Rightarrow x=a \\\ \end{aligned}$