Question

Through a point T, a tangent TA and a secant TPQ are drawn to a circle AQP. If the chord AB is drawn parallel to PQ, prove that the triangles PAT and BAQ are similar.

Answer 1

Hint:First of all, draw the diagram to visualize the question. Now use the alternate segment theorem to prove $\angle TAP$ equal to $\angle AQP$. Now use alternate angle theorem. Now, for any cyclic quadrilateral, the sum of the opposite angle is ${{180}^{o}}$. So use this and proceed further to prove two triangles equal by AA criteria.

Complete step-by-step answer:
Here, we are given that through a point T, a tangent TA and a secant TPQ are drawn to a circle AQP. If the chord AB is drawn parallel to PQ. We have to prove that the triangles PAT and BAQ are similar.

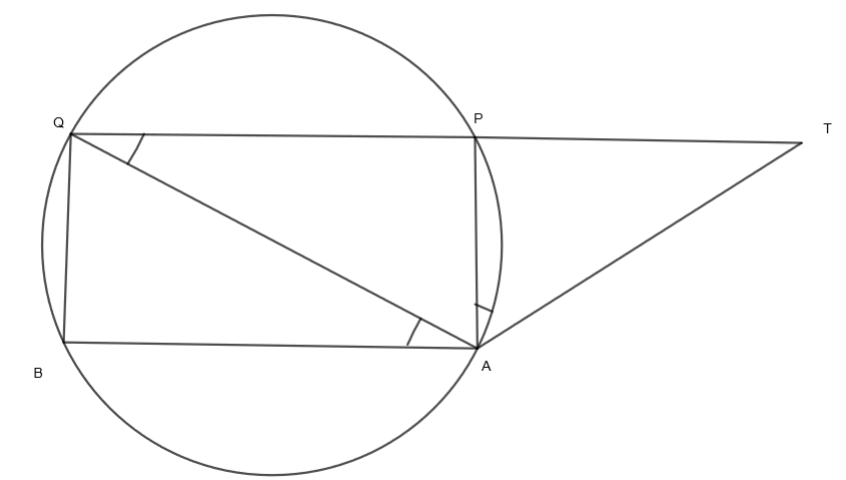
In the above figure, TA is the tangent and TPQ is a secant to the circle AQP. Also, AB is a chord that is parallel to PQ. We know that according to the alternate segment theorem, the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. Here, $\angle TAP$ is the angle between the tangent and the chord and $\angle AQP$ is its alternate segment angle. So, we get,
$\angle TAP=\angle AQP....\left( i \right)$
Now, we are given that AB is parallel to PQ. So, by alternate angle theorem, we get,
$\angle AQP=\angle QAB....\left( ii \right)$
From (i) and (ii), we get
$\angle TAP=\angle QAB....\left( iii \right)$
Now PQBA is quadrilateral inside the circle. So, PQBA is cyclic quadrilateral and we know that for any cyclic quadrilateral, the sum of the opposite angles is ${{180}^{o}}$. So, we get,
$\angle QPA+\angle QBA={{180}^{o}}$
$\angle QPA={{180}^{o}}-\angle QBA....\left( iv \right)$
Also, by the figure, we can see that,
$\angle QPA+\angle APT={{180}^{o}}$
$\angle QPA={{180}^{o}}-\angle APT$
By substituting the value of $\angle QPA$ from equation (iv), we get,
${{180}^{o}}-\angle QBA={{180}^{o}}-\angle APT$
By canceling the like terms, we get,
$\angle QBA=\angle APT.....\left( v \right)$
Now, let us consider the triangles $\Delta PAT$ and $\Delta BAQ$.
From equation (iii), we get,
$\angle TAP=\angle QAB$
Also, from equation (v), we get,
$\angle APT=\angle QBA$
So by angle-angle similarity criteria, $\Delta PAT$ and $\Delta BAQ$ are similar triangles.

Note: In this question, students must properly learn to use the alternate segment theorem by taking examples of the different figures. Also, for questions related to similar triangles or congruent triangles, always take care of the corresponding parts of the triangle like if $\Delta PAT$ is similar to $\Delta BAQ$, then $\angle P=\angle B,\angle A=\angle A$ and $\angle T=\angle Q$ are the necessary conditions.