Question

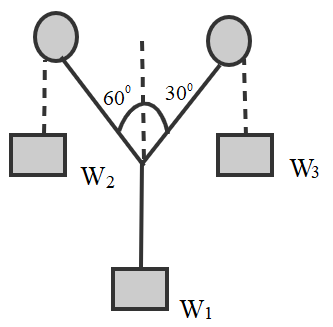
Three weights ${W_1}$, ${W_2}$ and ${W_3}$ hangs in equilibrium in figure assume Pulley ${P_1}$ and ${P_2}$ are frictionless, ${W_3} = 400\;{\rm{Newton}}$. Find the value of ${W_1}$ and ${W_2}$.

Answer 1

The above problem can be resolved using the concepts and the application of mechanics. The tension force will play a major role in identifying the magnitude of forces acting along with the weights. The tension forces can be calculated using the components of force, such that the vertical component is the tension force of the weights, respectively.

Complete step by step answer:
Given:
The value of ${W_3}$ is, ${W_3} = 400\;{\rm{Newtons}}$.
The angle of inclination with ${W_2}$ is ${\theta _1} = 60\;^\circ$.
The angle of inclination with ${W_3}$ is ${\theta _2} = 30\;^\circ$.
Let ${T_1}$ be the tension force balancing the weight ${W_3}$. Then apply the equilibrium condition as,

{T_1} = {W_3}\\\ {T_1} = 400\;{\rm{N}} \end{array}$$  Now, vertical component of force on $${W_2}$$ is, $${F_1} = {T_2}\sin {\theta _1}$$…………………………………. (1) Here, $${T_2}$$ is the tension force acting on the weight $${W_2}$$. Now, the vertical component of force acting on $${W_3}$$ is, $${F_2} = {T_1}\sin {\theta _2}.....................................\left( 2 \right)$$ Comparing the equation 1 and 2 as, $$\begin{array}{l} {F_1} = {F_2}\\\ {T_2}\sin {\theta _1} = {T_1}\sin {\theta _2} \end{array}$$ Solve by substituting the values as, $$\begin{array}{l} {T_2} \times \sin 60\;^\circ = {T_1} \times \sin 30\;^\circ \\\ {T_2} = \left( {400\;{\rm{N}}} \right) \times \dfrac{{\sin 30^\circ }}{{\sin 60\;^\circ }}\\\ {T_2} = \dfrac{{400}}{{\sqrt 3 }}\;{\rm{N}} \end{array}$$ The value of $${W_2}$$ is, $$\begin{array}{l} {W_2} = {T_2}\\\ {W_2} = \dfrac{{400}}{{\sqrt 3 }}\;{\rm{N}} \end{array}$$ And the value of $${W_1}$$ is, $$\begin{array}{l} {W_1} = {T_1} - {T_2}\\\ {W_1} = 400\;{\rm{N}} - \dfrac{{400}}{{\sqrt 3 }}\;{\rm{N}}\\\ {W_1} \approx 172\;{\rm{N}} \end{array}$$ Therefore, the value of $${W_1}$$ is 172 Newtons and value of $${W_2}$$ is $$\dfrac{{400}}{{\sqrt 3 }}\;{\rm{N}}$$. **Note:** To solve the given problem, we must know the technique to balance the forces acting along with the component. The arrangement having the pulley system and the string attached to it finds the application of two types of forces, namely the weight itself and the tension forces. The tension force is that magnitude of the force, that is utilised to transfer the linear to the machine element. Moreover, the tension force has significant applications in the analysis of machines also.