Question

Three waves of equal frequency having amplitudes 10mm, 4mm and 7mm arrive at a given point with successive phase difference $\dfrac{\pi }{2}$ . The amplitude of the resulting wave (in mm) given by:
A. 7
B. 6
C. 5
D. 4

Answer 1

Hint: Amplitudes of sinusoidally varying quantities behave as vectors and the phase difference act as angles between the vectors. So, we can add them in that method to find the amplitude of the resultant wave.

Complete step by step answer:
From the question, it is given that the three waves arrive at point with successive difference of ${{90}^{\circ }}$

So, consider that the amplitude of the first wave is along the x-axis, the second wave along y-axis and the third wave along the negative x-axis.

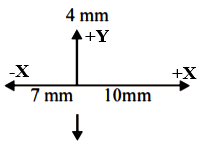
The waves of amplitude 10mm and 7mm will completely be out of phase and destructively interfere.
The amplitude of the resultant wave will be $10-7=3mm$
Let us now consider that the waves of amplitude 3mm and 4mm are out of phase by ${{90}^{\circ }}$
We shall apply the Pythagoras theorem to find the new amplitude of wave that will emerge when these two interfere with each other

${{A}^{2}}={{3}^{2}}+{{4}^{2}}$
${{A}^{2}}=25$
$A=5mm$

Therefore, the correct answer for the given question is option (C).

Note: There is another method to solve this question,
Consider the wave equations as

$\begin{aligned} & {{X}_{1}}=10\sin \left( \omega t \right) \\\ & {{X}_{2}}=4\sin \left( \omega t+\dfrac{\pi }{2} \right) \\\ & {{X}_{3}}=7\sin \left( \omega t+\pi \right) \\\ \end{aligned}$

On solving the phase difference, we get

$\begin{aligned} & {{X}_{2}}=4\cos \left( \omega t \right) \\\ & {{X}_{3}}=-7\sin \left( \omega t \right) \\\ \end{aligned}$

The disturbance according to the superposition theorem is calculated as

$\begin{aligned} & X={{X}_{1}}+{{X}_{2}}+{{X}_{3}} \\\ & X=10\sin \left( \omega t \right)+4\cos \left( \omega t \right)-7\sin \left( \omega t \right) \\\ & X=3\sin \left( \omega t \right)+4\cos \left( \omega t \right) \\\ \end{aligned}$

Let’s assume ‘R’ to be the resultant amplitude

$\begin{aligned} & 3=R\cos \phi \\\ & 4=R\sin \phi \\\ \end{aligned}$

Therefore, the equation becomes

$\begin{aligned} & X=R\cos \phi \sin \left( \omega t \right)+R\sin \phi \cos \left( \omega t \right) \\\ & X=R\sin \left( \omega t+\phi \right) \\\ \end{aligned}$

$R=\sqrt{{{3}^{2}}+{{4}^{2}}}=5mm$
The answer for the given question is option (C).