Solveeit Logo
Login

Question

Question: Three vectors \(\vec{A},\,\vec{B}\,\text{and}\,\vec{C}\) satisfy the relation \(\vec{A}.\vec{B}=0\) ...

Three vectors A⃗, B⃗ and C⃗\vec{A},\,\vec{B}\,\text{and}\,\vec{C} satisfy the relation A⃗.B⃗=0\vec{A}.\vec{B}=0 and A⃗.C⃗=0\vec{A}.\vec{C}=0. To which of the following vectors, vector A is parallel to?
A. B⃗.C⃗\vec{B}.\vec{C}
B. B⃗\vec{B}
C. C⃗\vec{C}
D. B⃗×C⃗\vec{B}\times \vec{C}

Explanation

Solution

When two vectors are parallel to each other, their dot product is zero.
The resultant vector obtained by cross product of two vectors is perpendicular to both of the vectors.
Use these properties of dot product and cross product of vectors to obtain the result.

Complete step by step answer:
Dot product of two vectors is product of their magnitudes and cosine of angle between them. The resultant dot product is scalar. Therefore, it is also known as a scalar product. Mathematically, we can write scalar product of two vectors a⃗\vec{a} and b⃗\vec{b} as
a⃗.b⃗= ∣a⃗∣∣b⃗∣cos⁡θ\vec{a}.\vec{b}=\,\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \theta
Where ∣a⃗∣\left| {\vec{a}} \right| and ∣b⃗∣\left| {\vec{b}} \right| is the magnitude of a⃗\vec{a} and b⃗\vec{b} respectively and θ\theta is the angle between them.
If the dot product of any two vectors is zero, then either one of the vectors is zero or both vectors are perpendicular to each other.
According to the question, A⃗.B⃗=0\vec{A}.\vec{B}=0 and A⃗.C⃗=0\vec{A}.\vec{C}=0
Therefore, we can conclude that A⃗\vec{A} is perpendicular to B⃗\vec{B} and A⃗\vec{A} is also perpendicular to C⃗\vec{C}. Mathematically,
A⃗⊥B⃗\vec{A}\bot \vec{B}
A⃗⊥C⃗\vec{A}\bot \vec{C}
The cross product of two vectors gives resultant vectors perpendicular to both the vectors.

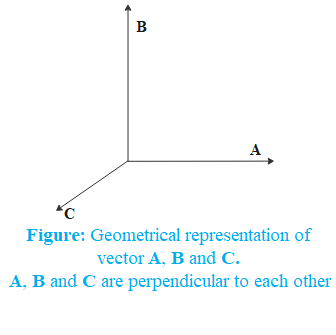
Therefore, resultant vector of cross product of vector B and vector C will be perpendicular to both vectors, B and C. Since vector A is also perpendicular to both the vectors B and C, it will lie in the same plane as the cross product B⃗×C⃗\vec{B}\times \vec{C}.
From the above statement, we can conclude that A⃗\vec{A} is parallel to B⃗×C\vec{B}\times C.

So, the correct answer is “Option D”.

Note: Dot product of two vectors is commutative i.e. a⃗.b⃗=b⃗.a⃗=abcos⁡θ\vec{a}.\vec{b}=\vec{b}.\vec{a}=ab\cos \theta .
Since any vector is parallel to itself, the dot product of a vector to itself is the magnitude squared of the vector i.e. (a⃗)2=a⃗.a⃗=a.a.cos⁡(0)=a2{{(\vec{a})}^{2}}=\vec{a}.\vec{a}=a.a.\cos (0)={{a}^{2}}
The dot product also follows distributive law i.e. a⃗.(b⃗+c⃗)=a⃗.b⃗+a⃗.c⃗\vec{a}.(\vec{b}+\vec{c})=\vec{a}.\vec{b}+\vec{a}.\vec{c}