Question
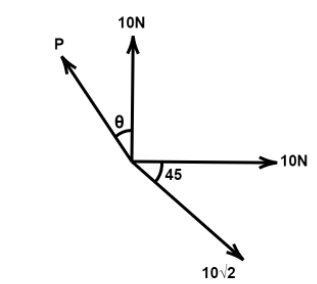
Question: Three vectors acts at a point O as shown in the figure, for the given values of P and \(\theta \) th...
Three vectors acts at a point O as shown in the figure, for the given values of P and θ the correct options are:-
(A) Resultant is null vector if θ=0,P=102
(B) Resultant is 10Nifθ=90∘,P=10N
(C) Resultant is 30i^Nif θ=23π,P=10Nin magnitude
(D) All are correct.
Solution
Hint A vector can be resolved into its components along the x and y axes. When they lie on the same axis, the vectors can be added or subtracted like normal numbers. The resultant of a vector can be found by adding two vectors.
Complete step by step solution
From the figure, it is clear that all the three vectors lie in a 2D plane. The correct option can be found by putting the value of P and θin each option. Suppose a vector makes angle θfrom an axis then the two components of this vector can be found by-
Multiplying the magnitude of the vector with the cos of the angle it makes with the axis. (for the base axis)
Multiplying the magnitude of the vector with the sin of the angle it makes with the axis. (for the perpendicular axis)
Resultant of two vectors is given by-
⇒ R=A2+B2+2ABcosθ
For two perpendicular vectors, cos90∘=0
R=A2+B2
For A, θ=0,P=102
The first step is to resolve all the components into i^ and j^components. Let those values be x and yrespectively. Then,
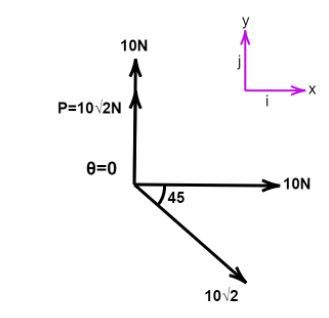
⇒ xi^=10i^+102cos45∘i^
⇒ \left\\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\\}
⇒ xi^=10i^+10i^=20i^
yj^=10j^+102j^−102sin45∘
⇒ yj^=102j^
⇒ \left\\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\\}
Resultant R=(xi^)2+(yj^)2
⇒ R=(20i^)2+(102j^)2
⇒ R=400+200
R=600=106
Resultant is not a null vector, statement is false.
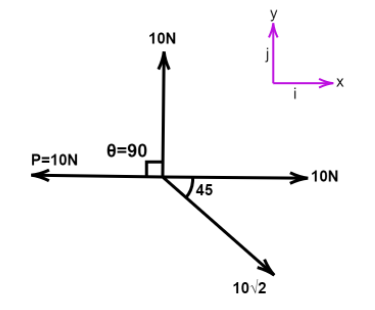
For B, θ=90∘,P=10N
xi^=10i^+102cos45∘i^−10i^
⇒ \left\\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\\}
⇒ xi^=10i^+10i^−10i^=10i^
⇒ yj^=10j^−102sin45∘j^
\left\\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\\}
yj^=10j^−10j^
yj^=0
Resultant, R=(xi^)2+(yj^)2
⇒ R=(10i^)2+(0j^)2+
⇒ R=100
R=10
Resultant is 10N, statement is true.
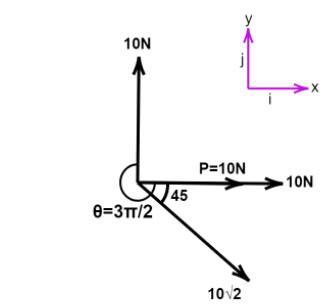
For C, θ=23π,P=10N
⇒ xi^=10i^+102cos45∘i^+10i^ ⇒ \left\\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\\}
⇒ xi^=10i^+10i^+10i^=30i^
yj^=10j^−102sin45∘j^
\left\\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\\}
yj^=10j^−10j^=0
Resultant, R=(xi^)2+(yj^)2
⇒ R=(30i^)2+(0j^)2
⇒ R=900=30
Resultant is 30N, since all the other components get cancelled out, the direction of this vector is on along x axis or i^, this statement is also true.
Hence the correct answers are option (B) and (C)
Note To find the resultant of multiple vectors, the best method is to resolve them into their x, y and z components and then find the resultant, this reduces the extra steps which would otherwise be required to find the angle made by the intermediate resultant vectors in the procedure.
