Solveeit Logo
Login

Question

Question: Three vectors \(7{ {\hat i}} - { {11\hat j}} + { {\hat k, 5\hat i}} + { {3\hat j}} - { {2\hat k, 12\...

Three vectors 7i^−11j^+k^,5i^+3j^−2k^,12i^−8j^−k^7{ {\hat i}} - { {11\hat j}} + { {\hat k, 5\hat i}} + { {3\hat j}} - { {2\hat k, 12\hat i}} - { {8\hat j}} - { {\hat k}} forms?
(1)\left( 1 \right) an equilateral triangle
(2)\left( 2 \right) an isosceles triangle
(3)\left( 3 \right) a right angled triangle
(4)\left( 4 \right) Collinear

Explanation

Solution

In this question, we have given three position vectors, by using them we will calculate the sides of the triangle then will calculate the magnitude of the sides and then check that the sides follow the conditions for which type of triangle. To specify the position of a point , we need to have a reference point and that reference point is called the position vector. For example: r⃗=xi^+yj^+zk^\vec r = x\hat i + y\hat j + z\hat k is a position vector where i^=\hat i = is a unit vector in the x-direction , j^=\hat j = is a unit vector in the y-direction and k^=\hat k = is a unit vector in the z-direction. The unit vectors are generally used to specify directions and are dimensionless quantities. A unit vector is calculated as : r^=r⃗∣r⃗∣=xi^+yj^+zk^x2+y2+z2\hat r = \dfrac{{\vec r}}{{\left| {\vec r} \right|}} = \dfrac{{x\hat i + y\hat j + z\hat k}}{{\sqrt {{x^2} + {y^2} + {z^2}} }} , where ∣r⃗∣\left| {\vec r} \right| is magnitude of the vector r .

Complete step by step answer:
Let vectors 7i^−11j^+k^,5i^+3j^−2k^and12i^−8j^−k^7{ {\hat i}} - { {11\hat j}} + { {\hat k, 5\hat i}} + { {3\hat j}} - { {2\hat k and 12\hat i}} - { {8\hat j}} - { {\hat k}} be the position vectors of points A , B and C respectively, i.e.
Let OA=7i^−11j^+k^{ {OA = 7\hat i}} - { {11\hat j}} + { {\hat k}} , OB=5i^+3j^−2k^{ {OB = 5\hat i}} + { {3\hat j}} - { {2\hat k}} and OC=12i^−8j^−k^{ {OC = 12\hat i}} - 8{ {\hat j}} - { {\hat k}} ;
Now, vectors AB⃗,BC⃗,AC⃗{ { \vec {AB}, \vec {BC}, \vec {AC}}} represent the sides of a triangle ABC.
The side AB⃗{ { \vec {AB}}} can be calculated as ;
⇒AB⃗=(5−7)i^+(3+11)j^+(−2−1)k^=−2i^+14j^−3k^\Rightarrow { { \vec {AB}}} = \left( {5 - 7} \right){ {\hat i}} + \left( {3 + 11} \right){ {\hat j}} + \left( { - 2 - 1} \right){ {\hat k}} = - 2{ {\hat i}} + { {14\hat j}} - 3{ {\hat k}}
Similarly, we can calculate BC⃗andAC⃗{ { \vec {BC} and \vec {AC}}} as follows ;
⇒BC⃗=(12−5)i^+(−8−3)j^+(−1+2)k^=7i^−11j^+k^\Rightarrow { { \vec {BC}}} = \left( {12 - 5} \right){ {\hat i}} + \left( { - 8 - 3} \right){ {\hat j}} + \left( { - 1 + 2} \right){ {\hat k}} = 7{ {\hat i}} - 11{ {\hat j}} + { {\hat k}}
⇒AC⃗=(12−7)i^+(−8+11)j^+(−1−1)k^=5i^+3j^−2k^\Rightarrow { { \vec {AC}}} = \left( {12 - 7} \right){ {\hat i}} + \left( { - 8 + 11} \right){ {\hat j}} + \left( { - 1 - 1} \right){ {\hat k}} = 5{ {\hat i}} + { {3\hat j}} - 2{ {\hat k}}
Now, let us calculate magnitudes of all the sides of the triangle;
⇒∣AB⃗∣=(−2)2+(14)2+(−3)2=4+196+9\Rightarrow \left| {{ { \vec {AB}}}} \right| = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {14} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {4 + 196 + 9}
⇒∣AB⃗∣=209\Rightarrow \left| {{ { \vec {AB}}}} \right| = \sqrt {209}
Similarly, the magnitudes of sides BC⃗andAC⃗{ { \vec {BC} and \vec {AC}}} can be calculated by ;
⇒∣BC⃗∣=(7)2+(−11)2+(1)2=49+121+1\Rightarrow \left| {{ { \vec {BC}}}} \right| = \sqrt {{{\left( 7 \right)}^2} + {{\left( { - 11} \right)}^2} + {{\left( 1 \right)}^2}} = \sqrt {49 + 121 + 1}
⇒∣BC⃗∣=171\Rightarrow \left| {{ { \vec {BC}}}} \right| = \sqrt {171}
And now,
⇒∣AC⃗∣=(5)2+(3)2+(−2)2=25+9+4\Rightarrow \left| {{ { \vec {AC}}}} \right| = \sqrt {{{\left( 5 \right)}^2} + {{\left( 3 \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt {25 + 9 + 4}
⇒∣AC⃗∣=38\Rightarrow \left| {{ { \vec {AC}}}} \right| = \sqrt {38}
Here, we can notice that ;
⇒∣BC⃗∣2+∣AC⃗∣2=∣AB⃗∣2\Rightarrow {\left| {{ { \vec {BC}}}} \right|^2} + {\left| {{ { \vec {AC}}}} \right|^2} = {\left| {{ { \vec {AB}}}} \right|^2}
By Pythagoras theorem, we know that in a right angled triangle ⇒(Base)2+(Perpendicular)2=(Hypotenuse)2 \Rightarrow {\left( {{ {Base}}} \right)^2} + {\left( {{ {Perpendicular}}} \right)^2} = {\left( {{ {Hypotenuse}}} \right)^2}
Means; (171)2+(38)2=(209)2{\left( {\sqrt {171} } \right)^2} + {\left( {\sqrt {38} } \right)^2} = {\left( {\sqrt {209} } \right)^2}
Hence, ΔABC\Delta { {ABC}} is a right angled triangle.
So, the correct answer is “Option 3”.

Note: Alternate method:
Step I : Check whether the sum of any two given vectors out of three generates the third vector or not. If this condition is satisfied then it is clear that the three given vectors form a triangle.
Given: A⃗=7i^−11j^+k^{ {\vec A = 7\hat i}} - { {11\hat j}} + { {\hat k}} , B⃗=5i^+3j^−2k^{ {\vec B = 5\hat i}} + { {3\hat j}} - { {2\hat k}} and C⃗=12i^−8j^−k^{ {\vec C = 12\hat i}} - 8{ {\hat j}} - { {\hat k}}
Notice that, A⃗+B⃗=(7i^−11j^+k^)+(5i^+3j^−2k^){ {\vec A}} + { {\vec B}} = \left( {{ {7\hat i}} - { {11\hat j}} + { {\hat k}}} \right){ { + }}\left( {{ {5\hat i}} + { {3\hat j}} - { {2\hat k}}} \right)
⇒A⃗+B⃗=(7+5)i^+(−11+3)j^+(1−2)k^\Rightarrow { {\vec A}} + { {\vec B}} = \left( {7 + 5} \right){ {\hat i}} + \left( { - 11 + 3} \right){ {\hat j}} + \left( {1 - 2} \right){ {\hat k}}
Which gives ; A⃗+B⃗=12i^−8j^−k^=C⃗{ {\vec A}} + { {\vec B}} = { {12\hat i}} - 8{ {\hat j}} - { {\hat k}} = { {\vec C}}
Hence, it is clear that the three given vectors form the sides of a triangle.

Step II : Now for a right angled triangle, we need to check which of the two vectors out of the given three vectors have an angle of 900{90^0} between them.
We know that two vectors are perpendicular to each other if their scalar or dot product is zero ;
As we have calculated above;
⇒AB⃗=−2i^+14j^−3k^\Rightarrow { { \vec {AB} = }} - 2{ {\hat i}} + { {14\hat j}} - 3{ {\hat k}}
⇒BC⃗=7i^−11j^+k^\Rightarrow { { \vec {BC} = }}7{ {\hat i}} - 11{ {\hat j}} + { {\hat k}}
⇒AC⃗=5i^+3j^−2k^\Rightarrow { { \vec {AC} = }}5{ {\hat i}} + { {3\hat j}} - 2{ {\hat k}}
The dot product of AB⃗andBC⃗{ { \vec {AB} and \vec {BC} }} can be calculated as;
⇒AB⃗⋅BC⃗=(−2i^+14j^−3k^)(7i^−11j^+k^)\Rightarrow { { \vec {AB}}} \cdot { { \vec {BC} = }}\left( { - 2{ {\hat i}} + { {14\hat j}} - 3{ {\hat k}}} \right)\left( {7{ {\hat i}} - 11{ {\hat j}} + { {\hat k}}} \right)
⇒AB⃗⋅BC⃗=−14−154−3=−171≠0\Rightarrow { { \vec {AB}}} \cdot { { \vec {BC} = }} - 14 - 154 - 3 = - 171 \ne 0
Hence, AB⃗andBC⃗{ { \vec {AB} and \vec {BC} }}are not perpendicular to each other.
Let us check for AB⃗andAC⃗{ { \vec {AB} and \vec {AC}}} ;
⇒AB⃗⋅AC⃗=(−2i^+14j^−3k^)(5i^+3j^−2k^)\Rightarrow { { \vec {AB}}} \cdot { { \vec {AC} = }}\left( { - 2{ {\hat i}} + { {14\hat j}} - 3{ {\hat k}}} \right)\left( {5{ {\hat i}} + { {3\hat j}} - 2{ {\hat k}}} \right)
⇒AB⃗⋅AC⃗=−10+42+6=38≠0\Rightarrow { { \vec {AB}}} \cdot { { \vec {AC} = }} - 10 + 42 + 6 = 38 \ne 0
Therefore, AB⃗andAC⃗{ { \vec {AB} and \vec {AC}}} are also not perpendicular to each other.
Now, check for BC⃗andAC⃗{ { \vec {BC} and \vec {AC} }} ;
⇒BC⃗⋅AC⃗=(7i^−11j^+k^)(5i^+3j^−2k^)\Rightarrow { { \vec {BC}}} \cdot { { \vec {AC} = }}\left( {7{ {\hat i}} - 11{ {\hat j}} + { {\hat k}}} \right)\left( {5{ {\hat i}} + { {3\hat j}} - 2{ {\hat k}}} \right)
⇒BC⃗⋅AC⃗=35−33−2=0\Rightarrow { { \vec {BC}}} \cdot { { \vec {AC} = 35}} - 33 - 2 = 0
∴BC⃗⋅AC⃗=0\therefore { { \vec {BC}}} \cdot { { \vec {AC} }} = 0
Therefore, BC⃗{ { \vec {BC}}} is perpendicular to AC⃗{ { \vec {AC}}} since their dot product or scalar product is zero means there is an angle of 900{90^0} between them. Therefore, the given vectors forms a right angled triangle as drawn below;

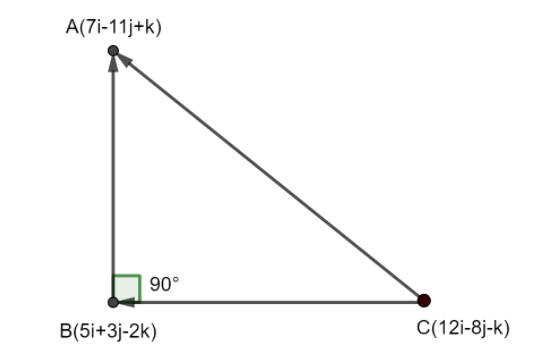
(1)\left( 1 \right) Dot product or scalar product: The scalar product of two vectors is the product of magnitudes of the two vectors and the cosine of the angle between them i.e. , the resultant value is always scalar in nature. (2)\left( 2 \right) Cross product or vector product: If θ\theta is the angle between the two vectors then cross product is given by : a×b=∣a∣∣b∣sin⁡θa \times b = \left| a \right|\left| b \right|\sin \theta , the resultant value is always vector in nature.