Question

Three uniform spheres, each having mass $m$ and radius $R$, are kept in such a way that each touches the other two, the magnitude of the gravitational force on any sphere due to the other two is
A. $\dfrac{{\sqrt 3 G{m^2}}}{{4{R^2}}}$
B. $\dfrac{{3G{m^2}}}{{4{R^2}}}$
C. $\dfrac{{\sqrt 3 G{m^2}}}{{{R^2}}}$
D. $\dfrac{{\sqrt 3 G{m^2}}}{{4{R^2}}}$

Answer 1

First to solve this problem we need to draw a rough diagram to solve this. As the three spheres are equal we can say that on joining their center it will form an equilateral triangle and the force on one sphere due to the other two are equal to each other. Then we need to calculate the resultant force as two forces are acting at angle to each other.

Complete step by step answer:
As per the problem we know that there are three uniform spheres, each having mass m and radius $R$, are kept in such a way that each touches the other two. Now we need to calculate the magnitude of the gravitational force on any sphere due to the other two.

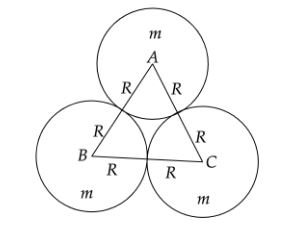
Here we know that forces acting on each of the spheres due to the third one are equal.Hence the two forces acting on the sphere A due to sphere B and C are equal to each other.Hence we can say,
${F_B} = {F_C}$
We know,
$F = \dfrac{{G{m_1} \times {m_2}}}{{{d^2}}}$
Where, gravitational force on the two bodies is $F$, mass of the two bodies are ${m_1}\,\,\,and\,\,{m_2}$ and distance between the two bodies is $d$.

Here three spheres are identical hence mass and radius are also same.
So, ${m_1} = {m_2} = m$ and $d = 2R$.
Now force on A due to B and C we will get,
${F_B} = {F_C} = \dfrac{{Gm \times m}}{{{{\left( {2R} \right)}^2}}}$
On further solving we will get,
${F_B} = {F_C} = \dfrac{{G{m^2}}}{{4{R^2}}}$
Hence two forces are acting at an angle then the resultant acting on the sphere.
Now we can write the resultant force magnitude as,
$F = \sqrt {{F_B}^2 + {F_C}^2 + 2{F_B} \times {F_C}\cos \theta }$

On putting the known value we will get,
$F = \sqrt {{{\left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)}^2} + {{\left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)}^2} + 2\dfrac{{G{m^2}}}{{4{R^2}}} \times \dfrac{{G{m^2}}}{{4{R^2}}}\cos 60^\circ }$
$\Rightarrow F = \sqrt {2{{\left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)}^2} + 2\dfrac{{G{m^2}}}{{4{R^2}}} \times \dfrac{{G{m^2}}}{{4{R^2}}} \times \dfrac{1}{2}}$
$\Rightarrow F = \sqrt {2{{\left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)}^2} + \dfrac{{G{m^2}}}{{4{R^2}}} \times \dfrac{{G{m^2}}}{{4{R^2}}}} = \sqrt {2{{\left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)}^2} + {{\left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)}^2}}$
Taking out the common terms from the root we will get,
$F = \left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)\sqrt {2 + 1}$
Hence the magnitude of force will be,
$\therefore F = \sqrt 3 \left( {\dfrac{{G{m^2}}}{{4{R^2}}}} \right)$

Therefore there are two correct options (A) and (D).

Note: On joining all the centers of the three spheres we will get an equilateral triangle as all the three spheres are identical to each other. On joining the radius we will get all the three sides as 2R. Hence we take the angle between the two forces as $60^\circ$. And remember that all the forces we have taken are acting on the center of the sphere.