Question

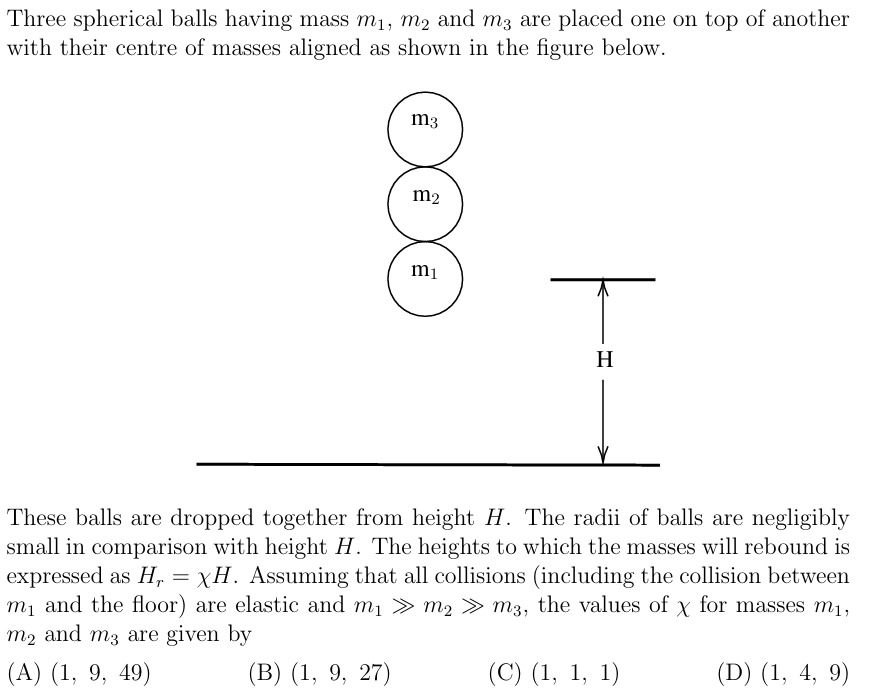
Three spherical balls having mass $m_1$, $m_2$ and $m_3$ are placed one on top of another with their centre of masses aligned as shown in the figure below.

These balls are dropped together from height $H$. The radii of balls are negligibly small in comparison with height $H$. The heights to which the masses will rebound is expressed as $H_r = \chi H$. Assuming that all collisions (including the collision between $m_1$ and the floor) are elastic and $m_1 \gg m_2 \gg m_3$, the values of $\chi$ for masses $m_1$, $m_2$ and $m_3$ are given by

• A. (1, 9, 49)
• B. (1, 9, 27)
• C. (1, 1, 1)
• D. (1, 4, 9)

Answer 1

Answer: (A)

(1, 9, 49)

Answer 2

The problem describes three spherical balls of masses $m_1$, $m_2$, and $m_3$ stacked vertically and dropped from a height $H$. We are given that all collisions are elastic and that $m_1 \gg m_2 \gg m_3$. We need to find the rebound heights for each mass, expressed as $H_r = \chi H$.

Let $v_0$ be the speed of the balls just before the first collision with the floor. From conservation of energy, $mgh = \frac{1}{2}mv^2$, so $v_0 = \sqrt{2gH}$. All balls initially move downwards with this speed.

We will analyze the collisions sequentially, using the property of elastic collisions between a very massive object ($M$) and a very light object ($m$), where $M \gg m$. If $U_M$ and $U_m$ are their initial velocities, and $V_M$ and $V_m$ are their final velocities, then for an elastic collision ($e=1$):

1. $V_M \approx U_M$ (the velocity of the massive object is almost unchanged).
2. $V_m \approx 2U_M - U_m$ (the velocity of the light object is approximately twice the velocity of the massive object minus its own initial velocity).

Step 1: Collision of $m_1$ with the floor

The floor can be considered an infinitely massive object.

Initial velocity of floor, $U_{floor} = 0$.

Initial velocity of $m_1$, $U_{m1} = -v_0$ (downwards).

After the elastic collision:

$V_{m1} \approx 2U_{floor} - U_{m1} = 2(0) - (-v_0) = v_0$.

So, $m_1$ rebounds upwards with a speed of $v_0$.

Step 2: Collision of $m_2$ with $m_1$

At the moment of this collision, $m_1$ is moving upwards with speed $v_0$, and $m_2$ is still moving downwards with speed $v_0$ (since the radii are negligible, $m_2$ hasn't hit $m_1$ yet).

Here, $m_1$ acts as the massive object ($M$) and $m_2$ as the light object ($m$).

Initial velocity of $m_1$, $U_{m1}' = v_0$ (upwards).

Initial velocity of $m_2$, $U_{m2} = -v_0$ (downwards).

After the elastic collision:

$V_{m1}' \approx U_{m1}' = v_0$. (Velocity of $m_1$ after colliding with $m_2$)

$V_{m2} \approx 2U_{m1}' - U_{m2} = 2(v_0) - (-v_0) = 3v_0$. (Velocity of $m_2$ after colliding with $m_1$)

So, $m_2$ rebounds upwards with a speed of $3v_0$.

Step 3: Collision of $m_3$ with $m_2$

At the moment of this collision, $m_2$ is moving upwards with speed $3v_0$, and $m_3$ is still moving downwards with speed $v_0$.

Here, $m_2$ acts as the massive object ($M$) and $m_3$ as the light object ($m$).

Initial velocity of $m_2$, $U_{m2}' = 3v_0$ (upwards).

Initial velocity of $m_3$, $U_{m3} = -v_0$ (downwards).

After the elastic collision:

$V_{m2}' \approx U_{m2}' = 3v_0$. (Velocity of $m_2$ after colliding with $m_3$)

$V_{m3} \approx 2U_{m2}' - U_{m3} = 2(3v_0) - (-v_0) = 6v_0 + v_0 = 7v_0$. (Velocity of $m_3$ after colliding with $m_2$)

So, $m_3$ rebounds upwards with a speed of $7v_0$.

Rebound Heights:

The height to which a mass rebounds is given by $H_r = \frac{V_r^2}{2g}$.

Since $v_0 = \sqrt{2gH}$, we have $v_0^2 = 2gH$. Therefore, $H = \frac{v_0^2}{2g}$.

For $m_1$:

Rebound velocity $V_{r1} = v_0$.

$H_{r1} = \frac{V_{r1}^2}{2g} = \frac{v_0^2}{2g} = H$.

So, $\chi_1 = 1$.

For $m_2$:

Rebound velocity $V_{r2} = 3v_0$.

$H_{r2} = \frac{V_{r2}^2}{2g} = \frac{(3v_0)^2}{2g} = \frac{9v_0^2}{2g} = 9H$.

So, $\chi_2 = 9$.

For $m_3$:

Rebound velocity $V_{r3} = 7v_0$.

$H_{r3} = \frac{V_{r3}^2}{2g} = \frac{(7v_0)^2}{2g} = \frac{49v_0^2}{2g} = 49H$.

So, $\chi_3 = 49$.

The values of $\chi$ for masses $m_1$, $m_2$, and $m_3$ are (1, 9, 49).