Question

Three sources of sound ${S_1}$ ​, ${S_2}$ ​ and ${S_3}$ ​ of equal intensity are placed in a straight line with ${S_1}{S_2} = {S_2}{S_3}$ ​(figure). At a point P, far away from the sources, the wave coming from ${S_2}$ ​ is $120^\circ$ ahead in phase of that from ${S_1}$ ​. Also, the wave combining form ${S_3}$ ​ is $120^\circ$ ahead of that from ${S_2}$ ​. What would be the resultant intensity of sound at P?

Answer 1

Hint Since the sources have equal intensity, they will have the same amplitude. So we need to calculate the phase of the different sources relative to ${S_2}$ and add the vectors of amplitude from these 3 sources at P to get the answer.

Complete step by step answer
We’ve been given that the three sources of sound have the same intensity so we know that they will have the same amplitude. At far away from the 3 sources, we’ve been given that the wave coming from ${S_2}$ ​ is $120^\circ$ ahead in phase of that from ${S_1}$ ​. Also, the wave combining form ${S_3}$ ​ is $120^\circ$ ahead of that from ${S_2}$.
Let us assume the amplitude of all the three waves as $A$ and the phase angle of ${S_2}$ as $\theta$. Since the wave coming from ${S_2}$ ​ is $120^\circ$ ahead in phase of that from ${S_1}$ ​ the phase angle of ${S_1}$ will be $\theta - 120^\circ$. Similarly, since the wave combing from ${S_3}$ ​ is $120^\circ$ ahead of that from ${S_2}$, the phase angle of ${S_3}$ will be $\theta + 120^\circ$
Then at point P, the amplitudes will be in the following form

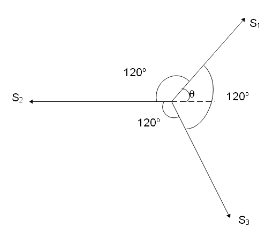
The amplitudes of the resultant vector due to these 3 vectors will cancel each other out in the following way. Let us take the amplitudes of all the 3 vectors in the direction of ${S_1}$ and in the direction perpendicular to ${S_1}$.
In the direction of ${S_1}$, the vector components of the amplitude will be
$A + A\cos 120^\circ + A\cos 240^\circ = A + A\left( {\dfrac{{ - 1}}{2}} \right) + A\left( {\dfrac{{ - 1}}{2}} \right)$
Which is equal to,
$= A - 2\left( {\dfrac{A}{2}} \right) = 0$
Similarly, in the direction perpendicular to ${S_1}$, the vector components of the amplitude will be
$\begin{gathered} = A\cos (120^\circ - 90^\circ ) + A\cos (240^\circ - 90^\circ ) \\\ = A\cos (30^\circ ) + A\cos (120^\circ ) \\\ \end{gathered}$
Substituting the proper values, we get
$\begin{gathered} = A\left( {\dfrac{1}{2}} \right) + A\left( { - \dfrac{1}{2}} \right) \\\ = 0 \\\ \end{gathered}$
Since the amplitude at point P is 0 in the direction parallel and perpendicular to ${S_1}$ the net amplitude of all the three sound waves combined is 0 and hence the intensity of the sound will be 0.

Note
In this question, the trick is to realize that the resultant sound intensity at P depends on the amplitude of the combination of all the 3 waves at point P which we calculated as 0 so the intensity is also 0 as the intensity of the sound wave is $\propto |A{|^2}$. The vector addition of 3 vectors that are oriented at an angle of $120^\circ$ to each other and have the same amplitude will be zero.