Question
Question: Three sources of emf \({V_0}\sin \omega t\) ,\({V_0}\cos \omega t\) , and \({V_0}\) are connected in...
Three sources of emf V0sinωt ,V0cosωt , and V0 are connected in series as shown. RMS value of current in the circuit is?
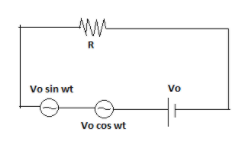
Solution
Here we have to use the concept of RMS values of AC and DC signals and finding out their Net value along with the use of Ohm's Law.
Formula used:
From ohms law the current I=RV
So, Irms=RVrms
For a sinusoidal AC source as Vrms=2V0
For the three different voltage sources the resultant of all these SRM voltages,
VnetRMS=(V1rms)2+(V2rms)2+(V3rms)2
Complete step by step answer:
Here we have to find the RMS value of current,
What we have here is some voltage sources and resistance. ohms will give us a relation connecting current and voltage.
So from ohm's law, we can calculate current as,I=RV
The term RMS stands for Root Mean Squared. The RMS value is the square root of the mean (average) value of the squared function of the instantaneous values. The symbols used for defining an RMS value are Vrms,Irms .
So, Irms=RVrms
To find Vrms , we have to consider each source and have to find Net Vrms in the circuit.
The sources V0sinωt and V0cosωt are sinusoidal AC sources with peaks at V0 . we know the value of Vrms for a sinusoidal AC source as Vrms=2V0
For DC source Vrms=Vdc
Since, we have, so we three different voltage sources here have to find resultant of all these SRM voltages,
VnetRMS=(V1rms)2+(V2rms)2+(V3rms)2
V1rms=Vdc=V0
V2rms=V3rms=Vac=2V0
Now substituting all these values in the Net RMS value of Voltage, we get
Vrms=(V0)2+(2V0)2+(2V0)2
Simplifying this equation,
Vrms=V02+2V02+2V02
=2V02
=2V0
Now we got the value of RMS voltage, so from this by using ohm's law we can find out Irms
Irms=RVrms=R2V0
So the answer is RV02.
Note:
If you have given some sinusoidal waveform, with the known value of its peak, then we can use these relations. Other than peak values, sometimes it may give average values or most probable values. That time, the equations will have some modifications.
