Question

Three solids of mass ${m_1}$ , ${m_2}$ and ${m_3}$ are connected with weight less string in succession and are placed on a frictionless table. If the mass ${m_3}$ is dragged with a force $T$ . The tension in the string between ${m_2}$ and ${m_3}$ is:-
(A) $\dfrac{{{m_2}}}{{{m_1} + {m_2} + {m_3}}}T$
(B) $\dfrac{{{m_3}}}{{{m_1} + {m_2} + {m_3}}}T$
(C) $\dfrac{{{m_1} + {m_2}}}{{{m_1} + {m_2} + {m_3}}}T$
(D) $\dfrac{{{m_2} + {m_3}}}{{{m_1} + {m_2} + {m_3}}}T$

Answer 1

Hint To solve this question, we have to determine the common acceleration of the whole system of the three masses. Then, by applying Newton's second and third laws we will get the final value of the required tension.

Formula Used: The formula used to solve this question is given by
$\Rightarrow F = ma$ , here $F$ is the force acting on a body of mass $m$ which is having an acceleration of $a$ .

Complete step by step answer
Consider the system of masses connected by strings in succession as shown in the figure below. Let the tension in the string between the masses ${m_1}$ and ${m_2}$ be ${T_1}$ and that between the masses ${m_2}$ and ${m_3}$ be ${T_2}$

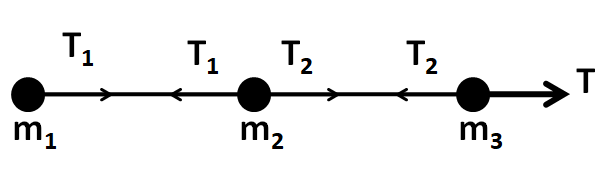
Let the common acceleration of the system be $a$ .
As we can clearly see, the only external force on this system is the force $T$ . So from the equation of the whole system we have,
$\Rightarrow F = T$ …………………………...(1)
Also, the total mass of this system is
$\Rightarrow M = {m_1} + {m_2} + {m_3}$ …………………………...(2)
So from the Newton’s second law of motion we have
$\Rightarrow F = Ma$
Putting the values from (1) and (2) we get
$\Rightarrow T = \left( {{m_1} + {m_2} + {m_3}} \right)a$
So we get the common acceleration of the system as
$\Rightarrow a = \dfrac{T}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}$ …………………………...(3)
Now, consider the free body diagram of the mass ${m_1}$ .

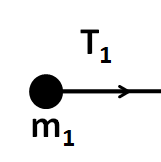
We can see that the net force on ${m_1}$ is
$\Rightarrow {F_1} = {T_1}$ …………………………...(4)
Also, its acceleration is equal to the acceleration of the system. So, from the Newton’s second law we get
$\Rightarrow {F_1} = {m_1}a$
From (3) and (4)
$\Rightarrow {T_1} = {m_1}\dfrac{T}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}$
$\Rightarrow {T_1} = \dfrac{{{m_1}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}T$ …………………………...(5)
Now, we consider the free body diagram of the mass ${m_2}$ .

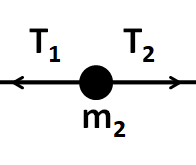
We can see that the net force on ${m_2}$ is
$\Rightarrow {F_2} = {T_2} - {T_1}$ …………………………...(6)
From the Newton’s second law we get
$\Rightarrow {F_2} = {m_2}a$
From (3) and (6) by substituting we get
$\Rightarrow {T_2} - {T_1} = {m_2}\dfrac{T}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}$
From (5) we can substitute the value of ${T_1}$ . So we get,
$\Rightarrow {T_2} - \dfrac{{{m_1}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}T = {m_2}\dfrac{T}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}$
Therefore the tension ${T_2}$ is
$\Rightarrow {T_2} = \dfrac{{{m_1}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}T + {m_2}\dfrac{T}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}$
On simplifying, we get
$\Rightarrow {T_2} = \dfrac{{{m_1} + {m_2}}}{{{m_1} + {m_2} + {m_3}}}T$
Therefore, the tension in the string connecting the masses ${m_2}$ and ${m_3}$ is equal to $\dfrac{{{m_1} + {m_2}}}{{{m_1} + {m_2} + {m_3}}}T$
Hence the correct answer is option C.

Note
Instead of considering the free body diagrams of the masses ${m_1}$ and ${m_2}$ , we could have considered that of the mass ${m_3}$ only. By applying Newton’s second law on the motion of the mass ${m_3}$ , we could have directly got the required value of the tension.