Question
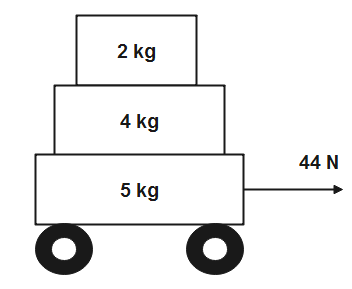
Question: Three slabs are stacked vertically with the lowest slab being on wheels as shown below. An applied f...
Three slabs are stacked vertically with the lowest slab being on wheels as shown below. An applied force of 44N acts horizontally on the bottom slab. How do you find the answer to the following question?
(a). What is the acceleration of the system if the blocks do not slip?
(b). How much friction acts between the bottom and the middle slab?
(c). What coefficient of friction is necessary to prevent slipping between the middle and bottom slab?
(d). How much friction is needed between the top and middle slab to prevent slipping?
Solution
Figure shows a system of three slabs kept over each other. If they do not slip, they move with the same velocity and acceleration. Using Newton’s second law, we can calculate the acceleration of the system. Also, the force compelling the slabs forward will be equal to the force of friction as the slabs do not slip.
Formulas used:
F=ma
Fr=μmg
Complete answer:
Given, three slabs are stacked on top of each other as shown in the figure.
(a). Since there is no slipping between the slabs, all three slabs are moving together. Therefore, the total mass of the system is- 2+4+5=11kg.
The force acting on the lowest slab is acting on the system as a whole. Therefore, as the Newton’s second law of motion says that,
F=ma - (1)
Here, F is the force applied
m is the mass of the system
a is the acceleration
In the above equation, given values are substituted to get,,
44=11×a⇒a=4ms−2
The system is accelerating at 4ms−2.
Therefore, the system is accelerating at 4ms−2 given that the slabs do not slip.
(b). Let us divide the figure into two systems; first system made of only the bottom slab, second system made of upper and the middle slab.
The acceleration of both systems is 4ms−2.
The mass of the second system will be-
4+2=6kg
From eq (1), the force acting on the second system will be-
F=6×4=24N
The friction force must be equal to 24N in the opposite direction to the motion due to which the slabs do not slip.
(c). The force of friction acting between the bottom and the middle slab is 24N. We know that, the force of friction is calculated as
Fr=μmg
Here, Fr is the force of friction
μ is the coefficient of friction
g is the acceleration due to gravity
In the above equation, given values are substituted to get,
24=μ×6×10⇒μ=0.4
Therefore, the coefficient of friction between the middle and the bottom slab is 0.4.
(d). Let us divide the figure into two systems; the first system is made of the lower and middle block while the second system is made of the top block.
Mass of the top block is 2kg and its acceleration is 4ms−2
Using eq (1), the force acting on the top block is
F=2×4=8N
Therefore, the force of friction acting between the top and the middle block is 8N in the opposite direction to the motion.
Note:
Friction opposes the motion of an object. According to Newton’s third law, the force in the direction of motion and the frictional force must be equal for the slabs to not slip. The coefficient of friction does have a unit. A constant force is acting on the system of slab and hence the acceleration is also constant.
