Question

Three Sets U, A and B have been given as:
$\begin{aligned} & Set U =1,2,3,4,5,6,7,8,9 \\\ & A=\\{x:x\in N,30<{{x}^{2}}<70\\} \\\ & B=\\{x:x\text{ is a prime number < 10}\\} \\\ \end{aligned}$
Find the values of $A',B',(A\cup B),(A'\cap B'),(A-B)'$.

Answer 1

In this problem, we have to find the element of Set A and Set B. After that, we have to analyze that both Set A and Set B are subsets of Set U. The complement of set refers to elements, not in that set.

Complete step-by-step solution:
We have been given that;
$Set U=1,2,3,4,5,6,7,8,9$
$A=\\{x:x\in N,30< {{x}^{2}}< 70\\}$
Here x is a natural number.
$\Rightarrow 30< {{x}^{2}}< 70$
We can split it into two cases:
Case 1: when $30< {{x}^{2}}$
$\begin{aligned} &\Rightarrow {{x}^{2}}> 30 \\\ & \Rightarrow {{x}^{2}}-30 >0 \\\ & \Rightarrow (x+\sqrt{30})(x-\sqrt{30})> 0 \\\ \end{aligned}$
Now, we will use a wavy curve method to get the values of x. According to the wavy curve method for quadratic polynomial, if a quadratic polynomial is given as $\left( x-\alpha \right)\left( x-\beta \right)$ , where $\alpha$ and $\beta$ are the zeroes, then the value of the polynomial $\forall x\in \left( \alpha ,\beta \right)$ will be less than zero and the value of the polynomial $\forall x\in \left( -\infty ,\alpha \right)\cup \left( \beta ,\infty \right)$ is greater than zero.
Now by using wavy curve method;
$(x+\sqrt{30})(x-\sqrt{30}) >0$

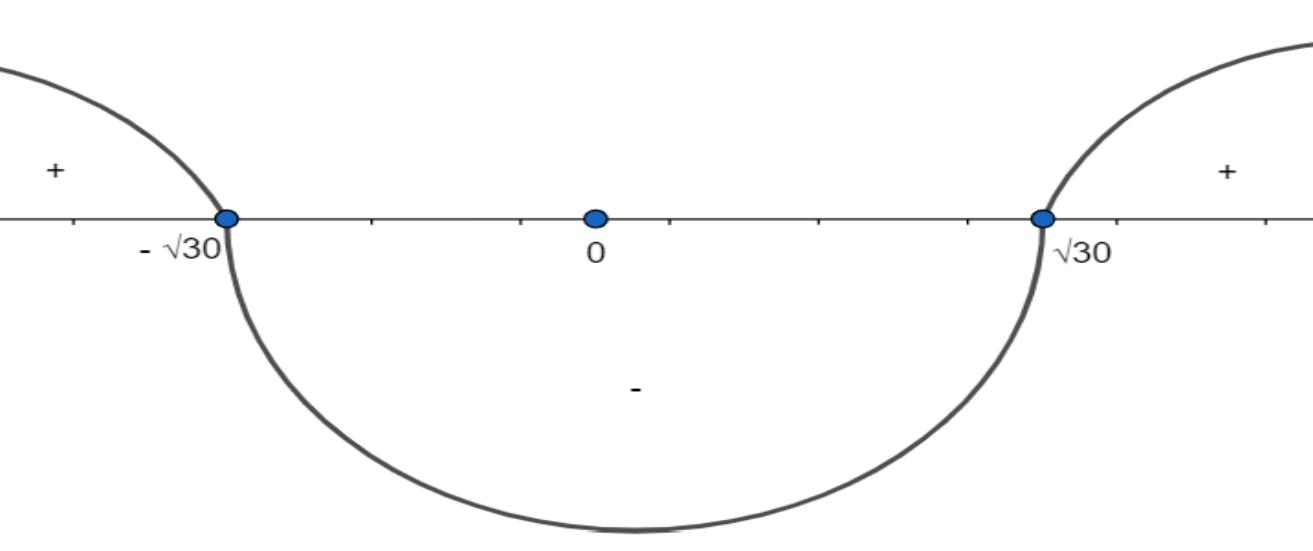
So, we have to find such value of x for which $(x+\sqrt{30})(x-\sqrt{30}) >0$, so using wavy curve, if we take any number from interval $(-\sqrt{30},\sqrt{30})$, we have $(x+\sqrt{30})(x-\sqrt{30})< 0$and if we take any value from interval $(-\infty ,-\sqrt{30})$ and $(\sqrt{30},\infty )$, we have $(x+\sqrt{30})(x-\sqrt{30}) >0$
So, we can say that for $(x+\sqrt{30})(x-\sqrt{30}) > 0$, we have
$\Rightarrow x>\sqrt{30}$ and $x< -\sqrt{30}............(1)$
Case 2: when ${{x}^{2}}< 70$
$\begin{aligned} &\Rightarrow {{x}^{2}} <70 \\\ & \Rightarrow {{x}^{2}}-70 <0 \\\ & \Rightarrow (x+\sqrt{70})(x-\sqrt{70}) <0 \\\ \end{aligned}$
By using wavy curve method;

So, we have to find such value of x for which $(x+\sqrt{70})(x-\sqrt{70}) <0$, so using wavy curve, if we take any number from interval $(-\infty ,-\sqrt{70})$ and $(\sqrt{70},\infty )$, we have $(x+\sqrt{70})(x-\sqrt{70})> 0$ and if we take any value from interval $(-\sqrt{70},\sqrt{70})$, we have $(x+\sqrt{70})(x-\sqrt{70}) <0$
So, we can say that for, we have
$-\sqrt{70}< x <\sqrt{70}........(2)$
Now we have two considering both case 1 and case 2. By wavy curve method, we have to take the intersection of equation (1) and (2) to get the value of x.
$\Rightarrow -\sqrt{70}< x <-\sqrt{30}$ and $\sqrt{30}< x < \sqrt{70}$
Here we have given that x is a natural number. So, we have to neglect all negative values of x.
$\therefore \sqrt{30}< x < \sqrt{70}$
Here given that x is a natural number. So, the possible value of x is 6, 7 and 8.
$x\in [6,7,8]$
$\Rightarrow A=\\{6,7,8\\}$
$B=\\{x:x\text{ is a prime number 10}\\}$
The prime numbers less than 10 are 2, 3, 5 and 7.
$\begin{aligned} & x\in [2,3,5,7] \\\ & \Rightarrow B=\\{2,3,5,7\\} \\\ \end{aligned}$
Here we can see that all elements of Set A and Set B belong to Set U. so we can say that Set A and Set B are subsets of Set U.
Now, we have to find A’ which means that elements belong to Set U but not Set A.
$\Rightarrow U=\\{1,2,3,4,5,6,7,8,9\\}$ and $A=\\{6,7,8\\}$
$\Rightarrow A'=U-A=\\{1,2,3,4,5,9\\}$
Now, we have to find B’ which means that elements belong to Set U but not Set B.
$\Rightarrow U=\\{1,2,3,4,5,6,7,8,9\\}$ and $B=\\{2,3,5,7\\}$
$\Rightarrow B'=U-B=\\{1,4,6,8,9\\}$
Now, we have to find $(A\cup B)$ which means elements either belonging to Set A or Set B.
$\Rightarrow A=\\{6,7,8\\}$ And $B=\\{2,3,5,7\\}$
$\Rightarrow A\cup B=\\{2,3,5,6,7,8\\}$
Now, we have to find $(A'\cap B')$ which means element common to both Set A’ and Set B’.
$\Rightarrow A'=\\{1,2,3,4,5,9\\}$ and $B'=\\{1,4,6,8,9\\}$
$\Rightarrow (A'\cap B')=\\{1,4,9\\}$
Now, we have to find$(A-B)'$. This can also be written as; $U-(A-B).........(3)$
Now, we have to find $(A-B)$ which means element present in Set A but not in Set B.
$\Rightarrow A=\\{6,7,8\\}$ and $B=\\{2,3,5,7\\}$
$\Rightarrow (A-B)=\\{6,8\\}$
We are putting the value of $(A-B)$ in equation (3).
$(A-B)'=U-(A-B)$
We get;
$\begin{aligned} & (A-B)'=U-\\{6,8\\} \\\ & \Rightarrow \mathsf{U}=\\{1,2,3,4,5,6,7,8,9\\} \\\ &\Rightarrow (A-B)'=\\{1,2,3,4,5,6,7,8,9\\}-\\{6,8\\} \\\ & \Rightarrow (A-B)'=\\{1,2,3,4,5,7,9\\} \\\ \end{aligned}$
Hence,
$\begin{aligned} & A'=\\{1,2,3,4,5,9\\} \\\ &\Rightarrow B'=\\{1,4,6,8,9\\} \\\ &\Rightarrow (A\cup B)=\\{2,3,5,6,7,8\\} \\\ &\Rightarrow (A'\cap B')=\\{1,4,9\\} \\\ &\Rightarrow (A-B)'=\\{1,2,3,4,5,7,9\\} \\\ \end{aligned}$

Note: In this problem, the biggest mistake is when we don’t analyze that Set A and Set B is a subset of Set U. We can directly find the value of Set A by putting some natural numbers i.e. 4, 5, 6, 7, 8, 9 and so on. So, we can see that only 6, 7, and 8 holds for Set A.