Question
Question: Three rods of material X and three rods of material Y are connected as shown in the figure. All the ...
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are identical in length and cross-sectional area. If the end A is maintained at 600 and the junction E at 100 , calculate the temperatures of the junctions B, C and D. The thermal conductivity of X is 0.92 CGS units and that of Y is 0.46 CGS units.
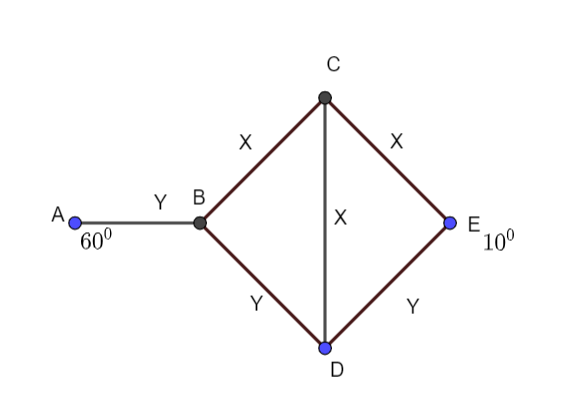
Solution
In this question, we will first derive a relationship between the thermal resistance of rod X and rod Y using the values of thermal conductivities given in the question. The difference in temperature is given by Δθ=IR where I is the current flowing in the system and R is the thermal resistance. For every arm we will calculate the net resistance and the current flowing through it and substitute the values in the physical relation and find the temperature of the junctions.
Complete step by step solution:
The thermal resistance of a rigid body is inversely proportional to the thermal conductivity of the material.
The mathematical expression is R∝K1 where R is the thermal resistance and K is the thermal conductivity.
For the rods X and Y we have,
RX∝KX1,RY∝KY1
Further simplifying this we have,
RYRX=KXKY
The thermal conductivity of X is 0.92 CGS units and that of Y is 0.46 CGS units.
KXKY=0.920.46
Further solving this we get,
KXKY=21
Hence, we can say that RYRX=KXKY=21
Let the resistance RX be R . The resistance RY will be 2R
Now the difference in temperature is given by Δθ=IR where I is the current flowing in the system and R is the thermal resistance.
Between A and B,
Suppose a current I is flowing.
The thermal resistance is equal to 2R .
So, the difference in temperature is given by θA−θB=2RI
It is given that θA=600
Hence, 600−θB=2RI
Between B and C,
The current gets divided at junction B. The current flowing in the arm BC is given by IBC=I×6R4R
The thermal resistance is equal to R .
So, the difference in temperature is given by θB−θC=32I
Between B and D,
The current gets divided at junction B. The current flowing in the arm BD is given by IBD=I×6R2R
The thermal resistance is equal to 2R .
So, the difference in temperature is given by θB−θD=32I
It can be noticed that θB−θD=θB−θC
Hence, we can say that junctions C and D are at the same temperature. So, the rod in the middle of the bridge will not carry any current.
The effective resistance between points A and E will be
Reff=R+Rbridge
Substituting the values, we get,
Reff=2R+2R+4R2R×4R
Further solving this equation, we get,
Reff=2R+34R
⇒Reff=310R
Between A and E,
The current flowing is equal to I.
The effective resistance is 310R
The difference in temperature is given by θA−θE=310RI
It is given that θA=600 and θE=100 .
⇒θA−θE=500
Substituting in the equation we get,
θA−θE=50=310IR
Further solving this we get,
IR=15
We calculated that 600−θB=2RI
Substituting the value, we get,
600−θB=2×15
Further solving this we get,
600−300=θB
⇒θB=300
We calculated that θB−θC=32I
Substituting the value, we get,
30−θC=32×15
Further solving this we get,
30−θC=10
⇒θC=200
The temperature of junctions C and D is same and so θD=200
Note: The term current can be misleading. Here it means thermal current. Thermal current is the flow of heat. The thermal system is synonymous as a whole with the electric system. The potential gradient is analogous to the temperature difference which acts as the driving force. The resistance is analogous to the thermal resistance while current to the thermal current.
