Question

Three rods made of the same material and having the same cross-section have been joined as shown in figure. Each rod is of the same length. The left and right ends are kept at ${0^0}C$ and ${90^0}C$ respectively. The temperature of the junction of the three rods will be

A. ${45^0}C$
B. ${60^0}C$
C. ${30^0}C$
D. ${20^0}C$

Answer 1

Generally when temperature difference is maintained then heat transfers from higher temperature body to the lower temperature body. The amount of heat transferred depends upon the various factors like the temperature difference, thermal resistance of the material.

Formula used:
\eqalign{ & R = \dfrac{L}{{KA}} \cr & H = \dfrac{{\Delta T}}{R} \cr}

Complete step by step answer:
Flow of a quantity with time is known as a current. It can be fluid current or heat current or electric current.
In case of fluid current a pressure difference is maintained and that drives the flow of fluid and fluid always flows from high pressure region to the low pressure region and fluid current is governed by fluid resistance too
Whereas in electric current the electric charge flows with time and the voltage difference and electric resistance combined will govern the electric current. Charge flows from higher voltage to lower voltage naturally.
Similarly in thermal current it is governed by temperature difference and thermal resistance.
Thermal resistance of a thermal conductor of length ‘L’ and cross sectional area ‘A’ and thermal conductivity ‘K’ is given by $R = \dfrac{L}{{KA}}$

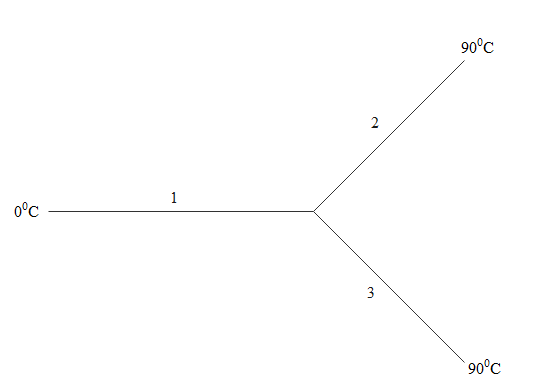
It is clearly evident that the right ends of rods 2 and 3 are at higher temperature than that of the left end of the first rod.
So the heat will flow from the 2 and 3 rods to the first rod. The heat can’t escape anywhere so the sum of rate of flow of heat from second and third rods will be equal to rate of flow of heat in the third rod. Let the junction temperature be ${x^0}C$. Rate of flow of heat is given by $H = \dfrac{{\Delta T}}{R}$. Where H is the rate of flow of heat and $\Delta T$ is the temperature difference between two ends of a conductor and $R$ is the thermal resistance which is given as $R = \dfrac{L}{{KA}}$ where L is the length of the conductor and K is the coefficient of heat conduction and A is the cross section area of the conductor. Thermal resistance for all three rods is the same. So the rate of flow of heat only depends on the temperature difference between the two ends of a conductor.
So sum of rate of flow of heat from second and third rods will be equal to rate of flow of heat in the third rod
\eqalign{ & {H_3} = {H_1} + {H_2} \cr & \Rightarrow \Delta {T_3} = \Delta {T_1} + \Delta {T_2} \cr & \Rightarrow x - 0 = (90 - x) + (90 - x) \cr & \Rightarrow 3x = 180 \cr & \therefore x = {60^0}C \cr}

Hence option 3 will be the correct answer.

Note:
As long as the temperature difference is maintained between the ends of the rods, the heat keeps on flowing. If the thermal resistance of the rods are different then the heat current will be depending on the length and area of cross section and thermal conductivity coefficients of all the conductors.