Question

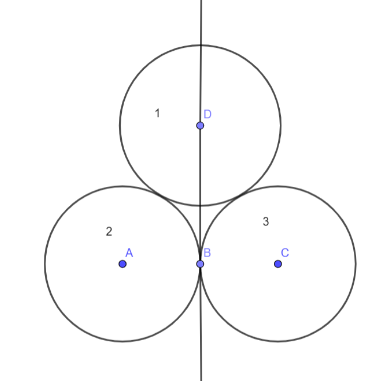
Three rings each of mass $M$ and radius $R$ are arranged as shown in the figure.The moment of inertia of the system about the axis is

A. $\dfrac{3}{2}M{R^2}$
B. $3M{R^2}$
C. $\dfrac{T}{2}M{R^2}$
D. $\dfrac{7}{2}M{R^2}$

Answer 1

The system consists of three rings each of which will contribute to the moment of inertia of the whole system about the given axis. For ring 1 the axis passes through the center and hence we can directly use the known formula. But for rings 2 and 3, we will use the parallel axis theorem since the axis is passing through the tangent in the plane of the ring. Then we will add the individual moment of inertia of each ring to get the moment of inertia of the whole system.

Formula used:
For a ring, the moment of inertia when the axis passes through the center is given as $I = \dfrac{{m{r^2}}}{2}$ where $m$ is the mass of the ring and $r$ is the radius of the ring. Also, the parallel axis theorem states that the moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of the body about the axis passing through the centre and product of the mass of the body times the square of the distance between the two axes. Mathematically, it is expressed as $I = {I_C} + m{h^2}$ where $h$ is the distance between the axis passing through the centre and the given axis and ${I_C}$ is the moment of inertia of the body when the axis passes through the centre.
If the axis is passing through the tangent in the plane of the ring, it will be given as,
$I = \dfrac{{m{r^2}}}{2} + m{r^2}$

Complete step by step answer:
The Moment of inertia of the system will be given by the sum of the moment of inertia of each ring about the axis.Hence,
$Z = {M_1} + {M_2} + {M_3}$
where ${M_i}$ is the moment of inertia of the ${i^{th}}$ ring with respect to the given axis.
Moment of inertia of ring 1 with respect to the axis is ${M_1} = \dfrac{{M{R^2}}}{2}$ since the axis is passing through the center.

For ring 2, the axis is passing through the tangent in the plane of the ring. Hence, the parallel axis theorem will be applied.The distance between the axis passing through the center of mass of ring 2 and the given axis is R.Hence, the moment of inertia of ring 2 with respect to the axis is,
${M_2} = \dfrac{{M{R^2}}}{2} + M{R^2}$
$\Rightarrow {M_2} = \dfrac{{3M{R^2}}}{2}$

For ring 3, the axis is passing through the tangent in the plane of the ring. Hence, the parallel axis theorem will be applied. The distance between the axis passing through the center of mass of ring 3 and the given axis is R.Hence, the moment of inertia of ring 3 with respect to the axis is,
${M_3} = \dfrac{{M{R^2}}}{2} + M{R^2}$
$\Rightarrow {M_3} = \dfrac{{3M{R^2}}}{2}$
The combined moment of inertia of the system is given by,
$Z = {M_1} + {M_2} + {M_3}$
Making proper substitutions, we get,
$Z = \dfrac{{M{R^2}}}{2} + \dfrac{{3M{R^2}}}{2} + \dfrac{{3M{R^2}}}{2}$
$\therefore Z = \dfrac{{7M{R^2}}}{2}$

Hence, option D is the correct answer.

Note: The parallel axis theorem is used for finding the moment of inertia of the area of a rigid body whose axis is parallel to the axis of the known moment body and it is through the centre of gravity of the object. In the parallel axis theorem, two mutually perpendicular moments of inertia are used for the calculations. This is determined by using the square of the distance from the axis of rotation. The moment of inertia of a body about its centre of mass is the least and increases with increasing distance.