Question

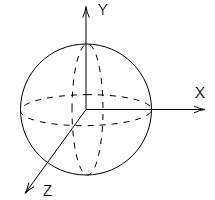
Three rings, each having equal radius $R$ are placed mutually perpendicular to each other and each having its centre at the origin of the coordinate system. If current $I$ is flowing through each ring, then the magnitude of magnetic field at the common centre is:

$(A)\sqrt 3 \dfrac{{{\mu _o}I}}{{2R}}$
$(B)0$
$(C)\left( {\sqrt 2 - 1} \right)\dfrac{{{\mu _o}I}}{{2R}}$
$(D)\left( {\sqrt 3 - \sqrt 2 } \right)\dfrac{{{\mu _o}I}}{{2R}}$

Answer 1

The acceleration of the centre of the mass of this particular system is calculated by using the vector equation of the acceleration of the two masses. The vector equation of both the blocks, that is, block $A$ and the vector equation of the block $B$ is used to find out the magnitude of the required acceleration of the centre of mass.

Complete step by step solution:
The magnetic field at the centre of the circular current carrying coil is given by the expression,
$\overrightarrow B = \dfrac{{{\mu _o}I}}{{2R}}$
Where,
${\mu _o}$ is the permeability constant
$I$ is the current flowing in the ring
$R$ is the radius of the ring
The magnetic field in the x-y plane due to the ring is,
$\overrightarrow {{B_1}} = \dfrac{{{\mu _o}I}}{{2R}}\widehat i$
The magnetic field in the y-z plane due to the ring is,
$\overrightarrow {{B_2}} = \dfrac{{{\mu _o}I}}{{2R}}\widehat j$
The magnetic field in the x-z plane due to the ring is,
$\overrightarrow {{B_3}} = \dfrac{{{\mu _o}I}}{{2R}}\widehat k$
The resultant of the magnetic field in all the three planes is given by the expression,
$\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} + \overrightarrow {{B_3}}$
On putting the required values, we get,
$\overrightarrow B = \dfrac{{{\mu _o}I}}{{2R}}\widehat i + \dfrac{{{\mu _o}I}}{{2R}}\widehat j + \dfrac{{{\mu _o}I}}{{2R}}\widehat k$
On taking $\dfrac{{{\mu _o}I}}{{2R}}$ as common,
$\overrightarrow B = \dfrac{{{\mu _o}I}}{{2R}}\left( {\widehat i + \widehat j + \widehat k} \right)$
Te magnitude of the above vector will be given by,
$\overrightarrow B = \dfrac{{{\mu _o}I}}{{2R}}\left( {\sqrt {1 + 1 + 1} } \right)$
$\overrightarrow B = \sqrt 3 \dfrac{{{\mu _o}I}}{{2R}}$
Thus, the magnitude of the magnetic field at the common centre is $\overrightarrow B = \sqrt 3 \dfrac{{{\mu _o}I}}{{2R}}$.
So, the correct answer is $(A)\sqrt 3 \dfrac{{{\mu _o}I}}{{2R}}$.

Note:
In this question, there were no turns present in the circular current carrying coil so, the expression for the magnetic field was given by the expression $\overrightarrow B = \dfrac{{{\mu _o}I}}{{2R}}$ but if there are $n$ turns present in the circular current carrying coil, then the expression for the magnetic field at the centre will be given by the expression $\overrightarrow B = \dfrac{{{\mu _o}nI}}{{2R}}$.