Question

Three resistors are connected in series across a 12V battery. The first resistor has a value of $1\Omega$, the second has a voltage drop of 4V, and the third has a power dissipation of 12W. Then, the value of the circuit current is
A) $2A$
B) $6A$
C) Either $2A$ or $6A$
D) None of the above

Answer 1

Ohm's law and power dissipated by the circuit expression used to solve the problem. Initially, the equivalent voltage across the resistance is calculated for a serious combination from using a given power value. Then current flow across the circuit is deduced by a quadratic equation.

Formula used:
The expression for finding the power is $P = VI$, Where $P$ is the power dissipated, $V$ is voltage and $I$ is the current.
According to the ohm's law, the expression for finding the voltage across the resistor is $V = IR$, Where $R$ is the resistance.

Complete step by step answer:
Let us first write the information given in the question.
$V = 12V,{R_1} = 1\Omega , {V_2} = 4V, {P_3} = 12W$
We have to find the current through the circuit.
The corresponding circuit diagram is similar to the following circuit.

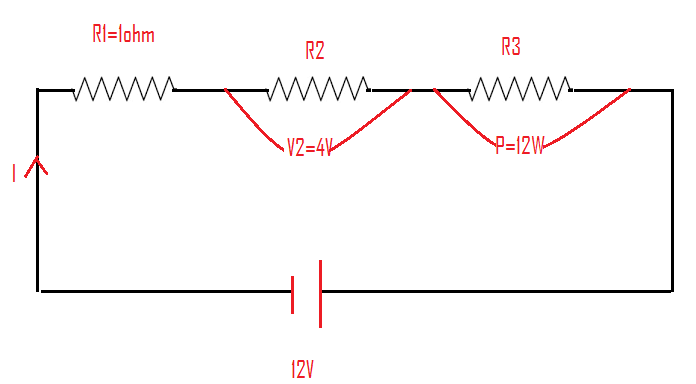
Let us now write the expression for the total voltage of the circuit.
$V = {V_1} + {V_2} + {V_3}$
Let us substitute the values in the above expression using $P = VI$ and $V = IR$
$\Rightarrow 12 = I \times 1 + 4 + \dfrac{{12}}{I}$
Let us now simplify the expression.
$\Rightarrow 12I = {I^2} + 4I + 12 \Rightarrow {I^2} - 8I + 12 = 0$
Let us use the middle term splitting to find the values of current.
$\Rightarrow {I^2} - 6I - 2I + 12 = 0$
Let us take the common terms from the first two and last two terms.
$\Rightarrow I(I - 6) - 2(I - 6) = 0$
Again, take common (I - 6) from the above terms.
$\Rightarrow (I - 6)(1 - 2) = 0$
Let us further solve for two values of current.
$I - 6 = 0 \Rightarrow I = 6A$ OR $I - 2 = 0 \Rightarrow I = 2A$

$\therefore$ The value of the current in the circuit is either 6A or 2A. Hence, the correct option is (C) is correct.

Note:
In series combination, the current is the same through every resistor but voltage varies. Hence, effective resistance is the sum total of all the resistors in the circuit.
In a parallel combination current is different through every resistor but voltage is the same across all the resistors as they are connected to the common potential difference. Hence, effective resistance is not just the sum of all resistors instead effective resistance gets reduced using the following formula.
$\dfrac{1}{{{R_{effective}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Where ${{\text{R}}_{\text{1}}}$ is the resistance of the first circuit and ${{\text{R}}_2}$ is the resistance of second circuit.