Question
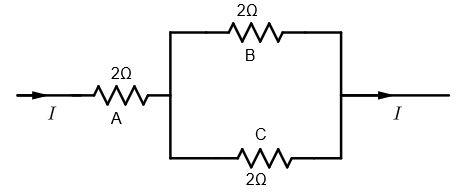
Question: Three resistors \(2\Omega\), A, B and C, are connected as shown in figure. Each of them dissipates e...
Three resistors 2Ω, A, B and C, are connected as shown in figure. Each of them dissipates energy and can withstand a maximum power of 18W without melting. Find the maximum current that can flow through the three resistors.
Solution
Use the formula for power dissipated by the resistor. Substitute Ohm’s law in it. Thus, you get a maximum current that can flow through a resistor A. Divide this value of current by 2 and get maximum current that can flow through three resistors.
Formula used:
P=RV2
V=IR
Complete step by step answer:
Given: R= 2Ω,
Power (P) = 18W
Power dissipated by the resistor is given by,
P=RV2 …(1)
where, P: Power dissipated by the resistor
V: Voltage across the resistor
R: Value of Resistance
According to Ohm’s Law,
V=IR …(2)
By substituting the equation. (2) in equation. (1) we get,
P=I2R
Rearranging the above equation we get,
I2=RP
∴I=RP …(3)
Now, by substituting values in equation.(3) we get,
∴I=218
∴I=3A
Thus, maximum current passing through resistor A is 3A.
The resistors B and C are connected in parallel hence, the current coming from resistor A is equally divided between resistors B and C.
Therefore, Current through B= Current through C = 21 Current through A
∴ Current through B= Current through C = 21×3
∴ Current through B= Current through C = 1.5A
Hence, the maximum current that can flow through three resistors is 1.5A.
Note:
As more and more resistors are connected in parallel in a circuit, the equivalent resistance of the circuit decreases while the total current of the circuit decreases. If the resistors B and C were connected in series then the current flowing through each resistor would be the same.
