Question

Three resistances, $1\Omega ,2\Omega ,3\Omega$ are connected in Series. What is the total resistance of the combination?
If the combination is connected to a $12{V}$ battery of negligible internal resistance, obtain the potential drop across each resistor.

Answer 1

The effective resistance of n Resistors of Resistances ${R_1},{R_2},{R_3} \cdot \cdot \cdot {R_n}$is ${R_{eff}} = {R_1} + {R_2} + {R_3} + \cdot \cdot \cdot + {R_n}$ . Also, when the current in a circuit is the same, the Resistances and Voltage across them follow a direct proportion.

Complete step-by-step answer:
We know that when three resistors- ${R_1}$ , ${R_2}$ , ${R_3}$ are connected in series, their effective resistance is given by : ${R_{eff}} = {R_1} + {R_2} + {R_3}$
Here, Since the resistances - ${R_1} = 1\Omega$ , ${R_2} = 2\Omega$ and ${R_3} = 3\Omega$ ${R_{eff}} = 1\Omega + 2\Omega + 3\Omega = 6\Omega$ .

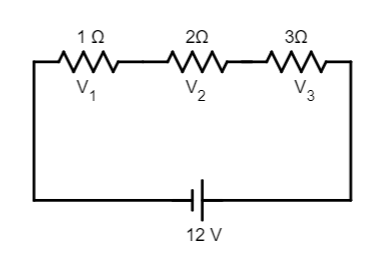
Now let's consider this combination of resistors being connected in series with a cell of $12V$ emf.

Since the cell is assumed to have zero internal resistance, the ends of the combination are directly connected to $12V$ emf and hence, the potential difference across the combination is $12V$ .
Let us now find the current passing through this circuit. Since the effective resistance of the combination is $6\Omega$ , The current in the circuit can be found using ohm's law as: $I = \dfrac{V}{R}$ Substituting values of $V$ and $R$ gives us : $I = \dfrac{{12}}{6} = 2A$
This $2A$ current is flowing through all three resistors since they are connected parallel.
Now, we are to find the potential drop across each resistor. So let the potential drop across resistors ${R_1}$ , ${R_2}$ , ${R_3}$ be ${V_1}$ , ${V_2}$ , ${V_3}$ respectively. Now ohm's Law tells us that the voltages ${V_1}$ , ${V_2}$ and ${V_3}$ are related to the current $I$ flowing through them and their resistances as-

$V = I \times R$ So ${V_1} = I \times {R_1} = 2 \times 1 = 2V$ ${V_2} = I \times {R_2} = 2 \times 2 = 4V$ ${V_3} = I \times {R_3} = 2 \times 3 = 6V$ So the potential difference across ${R_1}$ is $2V$ , ${R_2}$ is $4V$ , ${R_3}$ is $6V$ .

Additional Information:
we see that summing the voltage across all resistors - $2V + 4V + 6V$ , we get the emf of the cell. This is true for all closed loops in a Resistive circuit and called Kirchoff's voltage rule. Also, we can see that since the current is the same in a series circuit, Ohm's law simplifies to $V \propto R$ . So the total voltage $12V$ gets divided among the resistors in the direct ratio of their Resistance.

Note: For competitive examinations, calculations have to be simplified and hence, we can use the Direct proportionality between $V$ and $R$ to find the Voltages.
Since ${V_1}:{V_2}:{V_3}::1:2:3$
${V_1} = \dfrac{1}{{1 + 2 + 3}}{V_{tot}}$
${V_1} = \dfrac{1}{6}12V = 2V$
Similarly,
${V_2} = \dfrac{2}{6}12V = 4V$
${V_3} = \dfrac{3}{6}12V = 6V$