Question

Three prisms 1,2 and 3 have the prism angle A = 6°, but their refractive indices are, respectively 1.4, 1.5 and 1.6.If $\delta_1$, $\delta_2$, $\delta_3$, be their respective angles of deviation then :-

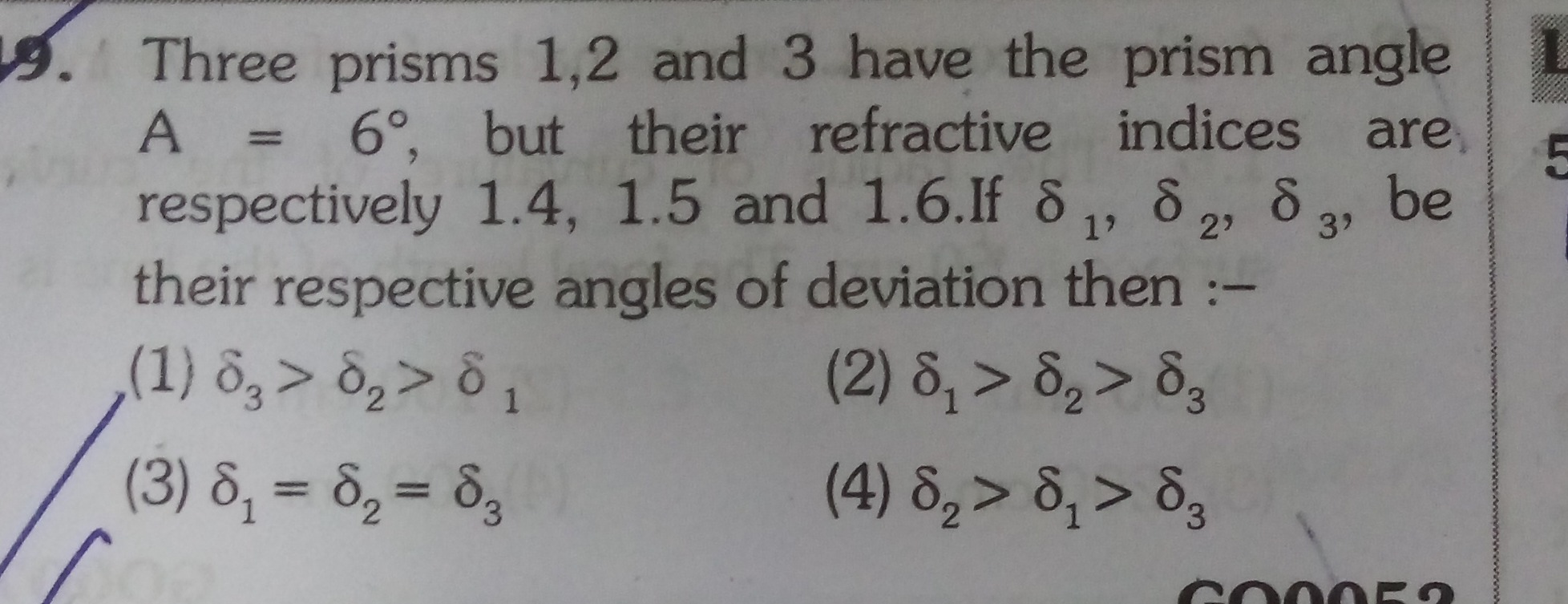
• A. $\delta_3 > \delta_2 > \delta_1$
• B. $\delta_1 > \delta_2 > \delta_3$
• C. $\delta_1 = \delta_2 = \delta_3$
• D. $\delta_2 > \delta_1 > \delta_3$

Answer 1

Answer: (A)

$\delta_3 > \delta_2 > \delta_1$

Answer 2

For a prism with a small prism angle $A$, the angle of deviation $\delta$ is given by the formula $\delta = (n-1)A$, where $n$ is the refractive index and $A$ is the prism angle. Since the prism angle $A$ is the same for all three prisms ($6^\circ$), the angle of deviation is directly proportional to the refractive index ($n$). Given that $n_1 = 1.4$, $n_2 = 1.5$, and $n_3 = 1.6$, we have $n_3 > n_2 > n_1$. Therefore, their respective angles of deviation will follow the same order: $\delta_3 > \delta_2 > \delta_1$.