Question

Three – point masses each mass $m$ are placed at the corners of an equilateral triangle of side $l$. The moment of inertia of the system about an axis coinciding with one side of the triangle is
A) $3m{l^2}$
B)$m{l^2}$
C)$\dfrac{3}{4}m{l^2}$
D)$\dfrac{2}{3}m{l^2}$

Answer 1

To find the moment of inertia of a system about an axis along any one side of the triangle. We will consider the axis passing through any one side of the triangle. Then on the basis of that we will find the moment of inertia of masses considering their perpendicular distance from the axis and then we will find the answer using formula $I = m{r^2}$.

Complete step by step answer:
In question it is given that three points pass each other of mass $m - ule$ placed at the corners of an equilateral triangle of side $a$, so first of all we will draw the figure for our simplicity.

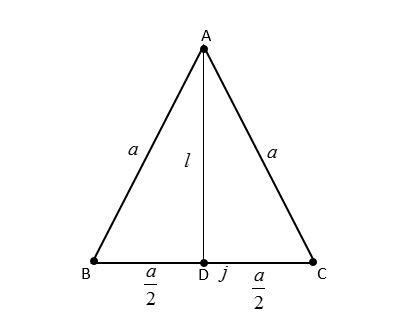
Now we will consider that axis passes through the side $BC$ Of the triangle $ABC$. Now, we know that the moment of inertia is given by the formula,
$I = m{r^2}$
Where, m is the mass of the body and l is the perpendicular distance of the mass from the axis
Now, on the basis of the formula we will find the perpendicular distance of masses from the axis. Now, we know that the masses which lie on the axis itself do not have perpendicular distance. So, now we will consider the mass lying at point $A$of the triangle.
Now, from the figure it can be seen that we can consider $\Delta ADC$, to find the perpendicular distance that is $AD$.
Let’s consider $AD$at $r$, $AC$is $a$ and $DC$is . by applying Pythagoras theorem, we will find $AD$, which can be given mathematically as,
$A{C^2} = A{D^2} + D{C^2}$
$\Rightarrow {a^2} = {r^2} + {\left( {\dfrac{a}{2}} \right)^2} \\\ \Rightarrow {a^2} - \dfrac{{{a^2}}}{4} = {r^2} \\\ \Rightarrow {r^2} = \dfrac{{4{a^2} - {a^2}}}{4} = \dfrac{{3{a^2}}}{4} \\\ \Rightarrow {r^2} = \dfrac{{3{a^2}}}{4} \\\$
Now, substituting the value pf ${r^2}$ in expression
(i) we will find the moment of inertia along the axis passing through $BC$, this can be given mathematically as,
$I = \dfrac{{m3{a^2}}}{4}$ $\Rightarrow I = \dfrac{{3m{a^2}}}{4}$
Thus, we can say that the moment of inertia of the system, an axis along one side of the triangle is $\dfrac{3}{4}m{a^2}$

So, the correct answer is “Option C”.

Note:
You can also consider the axis passing through side $AC$or side $AB$ of the triangle, as it will only change the terms in the equation but the final answer will remain the same.
You should not forget to use Pythagoras theorem for finding the perpendicular distance of mass $m$ at any side otherwise you won’t be able to find the answer.